Paper

Distributed Generation Analysis of a Microgrid System

Abstract

This paper examines the design and implementation of a microgrid system at Evertec, a financial technology company in Puerto Rico. The study focuses on integrating photovoltaic (PV) and combining heat and power (CHP) systems to address the challenges of high electricity costs and grid instability. A comprehensive analysis, supported by simulations, evaluates the energy output, economic feasibility, and sustainability of the system. Key findings demonstrate the PV system’s efficiency in utilizing Puerto Rico’s abundant sunlight and the CHP system’s ability to provide stable, cost-effective energy. These results underscore the potential of hybrid microgrids in enhancing energy resilience and reducing costs.

Introduction

Evertec, a prominent leader in financial technology services in Puerto Rico, faces persistent energy challenges, including prohibitively high electricity costs and an unreliable power grid. In response to these pressing issues, the company has explored innovative alternatives, such as microgrid systems that integrate renewable and conventional energy sources. This paper focuses on the design and implementation of a hybrid microgrid that combines photovoltaic (PV) systems and combined heat and power (CHP) technologies. By capitalizing on Puerto Rico’s abundant solar resources and incorporating advanced cogeneration methods, the proposed system seeks to deliver cost-effective, reliable energy while significantly reducing greenhouse gas emissions.

CHP systems, often referred to as cogeneration systems, represent a highly efficient approach to energy production. These systems generate electricity while simultaneously capturing and utilizing waste heat for practical applications such as space heating, water heating, and industrial processes. This dual-purpose capability greatly enhances overall energy efficiency compared to producing electricity and heat independently. Typically fueled by natural gas or biomass, CHP systems include components such as turbines, heat exchangers, and steam generators. The increasing adoption of CHP technologies reflects growing concerns about energy efficiency, sustainability, and the need to mitigate environmental impacts.

In parallel, PV systems harness sunlight to generate electricity through semiconductor materials embedded in solar panels. These systems are complemented by components such as inverters, which convert direct current (DC) into alternating current (AC), and batteries that provide energy storage to enhance system reliability. Particularly effective in regions with high solar irradiance, such as Puerto Rico, PV systems reduce reliance on traditional energy sources while minimizing environmental footprints. Recent advancements in solar technology have further improved the efficiency, scalability, and economic viability of PV systems, making them an essential component of modern energy solutions.

Moreover, by integrating PV and CHP systems into a cohesive microgrid, Evertec aims to reduce dependency on the utility grid, achieve significant long-term cost savings, and enhance overall energy reliability. This paper presents a comprehensive technical and economic analysis of the proposed system, highlighting its capacity to address Evertec’s energy challenges while ensuring financial sustainability. Ultimately, the findings contribute to broader discussions about adopting resilient and sustainable energy solutions, particularly in regions facing similar economic and infrastructural constraints.

PV Generation System Design

Evertec’s photovoltaic design in Cupey, PR diverges from traditional commercial designs by prioritizing the number of photovoltaic modules that can be integrated into the multi-level parking facility and regular parking spaces. The areas to be discussed are shown in Figure 1.

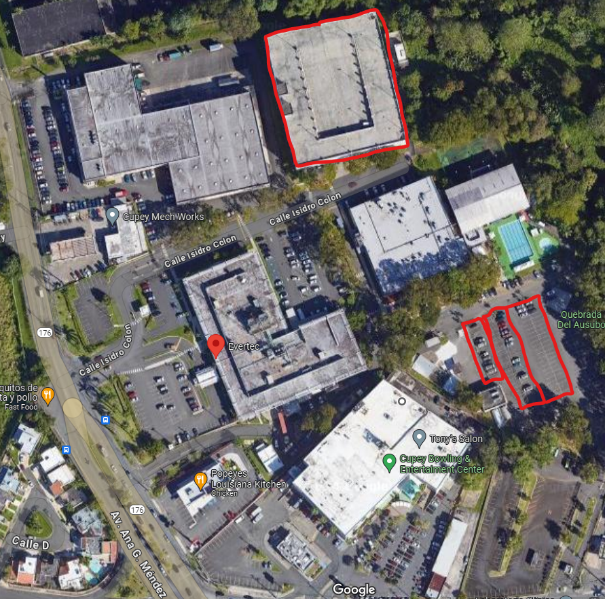
Figure 1: Evertec Workspaces

Multiply the length (L) and the width (W) to determine the area. In equation 1, the formula for measuring an area is as follows.

$ A = LW \ \text{(Equation 1)} $

Figure 2: Multi-Level Parking Segments

The previously calculated area values are summarized in table 1 below.

Description	Multi-Level Parking	Ground-Level Parking
Original Roof Area	56,270.55 ft^2	19,942.4 ft^2
RED Segment	7,792.8 ft^2	N/A
YELLOW Segment	10,263.2 ft^2	N/A
PURPLE Middle Segment	7,993.35 ft^2	N/A
PURPLE Corner Segments	5,684.16 ft^2	N/A
ORANGE Segments	3,513.92 ft^2	N/A
Area Considering 3ft Fire Line	N/A	19,936.4 ft^2
Total Usable Space	35,247.4 ft^2	19,936.4 ft^2

Table 1: Area Values Summary

Towards the guarantee of optimal performance and cost-effectiveness, it is necessary to evaluate a variety of factors when selecting a PV module (Canadian Solar BiHiKu6 Bifacial Mono 550W) for a solar system. These factors include both mechanical and electrical characteristics. Voltage, current, and power output are critical electrical characteristics. The module’s energy production capacity is determined by these parameters.

Furthermore, the selection process is significantly influenced by factors such as price, availability, and warranty. Mechanical considerations are equally significant. Installation and long-term durability are contingent upon the structural integrity, weight, and dimensions of the module. Reliability and safety necessitate the capacity to endure mechanical stresses, including snow and wind. The selection process prioritizes efficacy in power generation, mitigating losses, and competitive pricing, given the diverse range of PV modules available. Energy production is maximized by modules that provide a high-power output per hour of sunlight. Modules with a high-power output are prioritized due to the absence of energy production constraints in this endeavor. Effectively satisfying the project’s requirements, the selected PV module must achieve a proportion between cost-effectiveness, mechanical robustness, and electrical performance.

Achieving comprehension of the technical specifications, performance under diverse conditions, conformance with standards, warranty terms, installation guidelines, and system integration of a PV module, it is crucial to consult its datasheet (refer to figures 3 and 4). It enables users to make informed decisions, ensures proper utilization, and enables comparison with other modules.

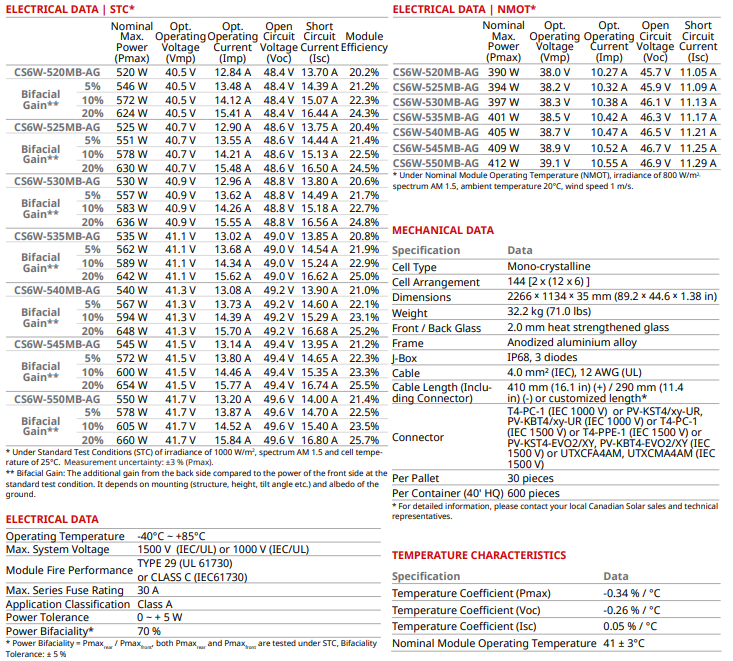
Figure 3: Solar Module Data

Figure 4: Solar Module Data Curves

In addition, the available space for the Evertec company PV system design will be divided into Ground-Level Parking and Multi-level Parking segments, as illustrated below. This will result in two distinct surface areas. The purpose of preventing system frequency and voltage stability issues, the power output of the solar array must be restricted to less than 1 MW, as the client has no interest in investing in a battery backup system. Consequently, the PV system will not provide complete coverage of Evertec’s energy consumption. The quantity of PV modules necessary will be determined by utilizing a minimum guaranteed solar array DC power output of 750,000Wdc in the calculations. The client specifically needs close to 600,000Wac for the system to run independently from the grid. The capability to verify whether there is sufficient space for the quantity of PV modules necessary to generate 750,000Wdc, it is necessary to first determine the number of PV modules that can be installed in each segment of the roof by utilizing the available surface area.

$ Module A = \frac{A_{FA}}{A_M} \ \text{(Equation 2)} $

Where:

$ A_{FA} = \text{Final Area of Multi-Level Parking’s Roof} $
$ A_{M} = \text{Area Per Module} $

The usable surface area of the roof of the multi-level parking facility, as illustrated in table 3. The length and width of each PV module are demonstrated in table 2. The information was available in the manufacturer’s data document, which was previously displayed. After converting to feet, these are the final values.

Description	PV Module Size (in)	PV Module Size (ft)
Length	89.2	7.4
Width	44.6	3.7

Table 2: Module Sizes

Description	Multi-Level Parking	Ground-Level Parking
Total Usable Space	35,247.4 ft^2	19,936.4 ft^2

Table 3: Available Space

Equation 2 can be used to determine the total number of PV modules for the roof’s multi-level parking.

$ Modules = \frac{35,247.4ft²}{{(7.4ft)}{(3.7)}}=1,287 $

Consequently, the total number of PV modules for the multi-level parking is 1,287, as determined by the available surface area of the roof.

$ Module B = \frac{A_{FB}}{A_M} \ \text{(Equation 3)} $

Where:

$ A_{FB} = \text{Final Area of Ground-Level Parking} $
$ A_{M} = \text{Area Per Module} $

Equation 3 can be used to determine the total number of PV modules for ground-level parking referencing the values in table 3.

$ Modules = \frac{19,936.4ft²}{{(7.4ft)}{(3.7)}}=728 $

Consequently, the total number of PV modules is 728, as determined by the available surface area on the ground-level parking.

Currently, utilizing equation 4 to determine the necessary quantity of PV modules to generate the minimum guaranteed solar array power output of 750,000Wdc. These calculations will be conducted using the datasheet for the Canadian Solar BiHiKu6.

$ N = \frac{P_{arr-g}}{A_{mpp}} \ \text{(Equation 4)} $

Where:

$ N = \text{total number of PV modules} $
$ P_{arr-g} = \text{Power guaranteed from the solar array without losses} $
$ P_{mpp} = \text{Power produced per PV module} $
$ N = \frac{750,000W}{550W} = 1363 $

Consequently, 1,363 PV modules are necessary to achieve a minimum guaranteed solar array power output of 750,000Wdc. Following simulations conducted on Helioscope, the solar array panels will be split to optimize the limited area available. The solar array will consist of 1,224 PV modules for the multi-level parking and 139 for the ground-level parking, as Evertec’s areas are divided into two. There is sufficient surface area to accommodate the specified number of PV modules per parking space.

It is imperative to choose the appropriate inverter for a photovoltaic system in order to ensure its efficacy, performance, and longevity. It is crucial to consider the following parameters when selecting this device:

Nominal Power (kW): The nominal power of the inverter should correspond to the output capacity of the solar panels. Considering the potential future expansions of the system, it is crucial to guarantee that the inverter has the necessary capacity to manage the utmost power generated by the solar panels.
Energy efficiency: The efficacy of inverters is essential, as it dictates the amount of solar energy that is converted into usable electricity. High-efficiency inverters can optimize energy production and minimize conversion losses.
Maximum Power Point Tracking (MPPT): Inverters that utilize MPPT technology continuously modify the electrical capacity to optimize energy production, even in the presence of variable solar conditions. In order to guarantee maximum system performance, it is essential to use an inverter equipped with a dependable MPPT algorithm.
Protection toward Overvoltage and Short Circuits: Inverters must be equipped with robust protection features to mitigate the risks of damage from overvoltage, short circuits, or other adverse conditions and ensure the safety of the system.
Durability and Reliability: It is crucial to choose an inverter from a reputable manufacturer that provides a sufficient warranty and high-quality products. The longevity of the inverter is essential for the uninterrupted operation of the photovoltaic system.
Monitoring Systems Compatibility: Certain inverters are equipped with integrated monitoring functions that enable the monitoring of system performance in real time. Effective system administration and maintenance may necessitate the capacity to establish connections to external monitoring systems.

	SMA	Growatt	Ginlong
Model	TRIPOWER CORE1 62-US	MAC 70KTL3-X MV	Solis-100K-5G-US
Power Ratings	62,500 W	70,000 W	100,000 W
Efficiency	98%	98.8%	98.80%
MPP Trackers	6	3	10
Price	6,700.00	3,700.00	7,000.00

Table 4: Inverter Characteristics

Upon analyzing the aforementioned table, the inverter that most accurately meets the specified requirements is the SMA Sunny Tripower 62-US, as it delivers optimal output power and accommodates a respectable number of strings per input. The disadvantage of these systems is their high price, necessitating more inverters; nevertheless, in the event of an inverter failure, a substantial percentage of power production will not be lost.

Additionally, it is crucial to evaluate the inverter’s capacity in series, parallel, maximum current, and maximum power, in addition to comparing the parameters. To accomplish this, the Datasheet of the equipment is illustrated in figures 5 and 6, which demonstrate that it continues to satisfy the essential specifications for t project.

Figure 5: String Inverter Model Description

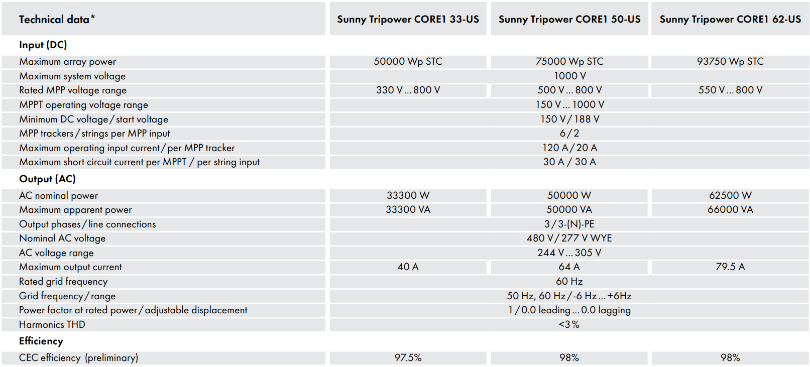
Figure 6: String Inverter Datasheet

The quantity of inverters required for the design will be examined in this section. A series connection is the optimal solar panel configuration for this undertaking prior to commencing the calculations. This suggests that the direct current (DC) output of one panel is connected to the next panel, thereby increasing the total system voltage, as all panels are electrically connected in series. The inverter is subsequently connected to this chain. As previously mentioned, this configuration offers several benefits, such as an increase in system voltage, which reduces wiring losses, provides design flexibility, and improves system performance. The subsequent step will involve determining the quantity of inverters necessary for the undertaking. Accomplishing this requires a specific value from the technical datasheets of the PV module and the designated inverter, as detailed in the preceding sections. Table 5 and Table 6 respectively reflect this information.

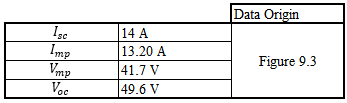
Table 5: PV Module Specifications

Initially, the utmost number of solar modules that can be connected in series for a specific inverter is denoted by equation 5. The process divides the open circuit voltage of the photovoltaic module by the maximal system voltage of the inverter in Table 5. This guarantees that the inverter’s utmost permissible voltage is not exceeded by the string’s total voltage.

$ \text{Modules per string} = \frac{V_{Inom}}{V_{OC}} \ \text{(Equation 5)} $

Where:

$ V_{Inom} = \text{Inverter nominal system voltage} $
$ V_{OC} = \text{PV module open circuit voltage} $
$ \text{Modules per string} = \frac{800V}{49.6V} = 17 $

The subsequent stage, as illustrated in Equation 6, is to determine the total power of a series of solar modules for the photovoltaic system. The energy generation capacity of the string is determined by multiplying the nominal power of a single module in figure 3 by the total number of modules in per string Equation 5.

$ \text{Power per string} = (\text{Module per string})*(\text{Module power}) \ \text{(Equation 6)} $
$ \text{Power per string} = 16*550W=9,350W $

Equation 7 subsequently determines the greatest number of solar module strings that can be connected to a single inverter. The maximal power output of the inverter is divided by the total power output of a series of modules in this calculation, as determined by Equation 6. This phase is essential for the proper scaling of the system and the prevention of inverter saturation is reached.

$ \text{String per Inverter} = \frac{\text{Maximum Iverter Power}}{\text{Power per String}} \ \text{(Equation 7)} $
$ \text{String per Inverter} = \frac{75,000W}{9,350W} = 8 $

Consequently, equation 8 gives the total number of solar modules that can be connected to a single inverter in a photovoltaic system. This quantity is determined by multiplying the number of modules per string as determined by Equation 5, by the number of threads per inverter as determined by Equation 7. To prevent the inverter from being overloaded and to ensure that the system is properly sized, this process is extremely important.

$ \text{Modules per inverter} = \text{Modules per sting} * \text{Sting per inverter} \ \text{(Equation 8)} $
$ \text{Modules per inverter} = 16 * 8 = 136 $

In summary, equation 9 calculates the total number of inverters required in the photovoltaic system by examining the total number of solar modules in equation 9.4 and the number of modules that can be connected to a single inverter in equation 8. The efficient utilization of the available inverters is contingent upon this calculation.

$ \text{Inverter Quantity} = \frac{\text{Total Moudles Needed}} {\text{Modules per Inverter}} \ \text{(Equation 9)} $
$ \text{Inverter Quantity} = \frac{1360} {136} = 10 $

Therefore, the PV system necessitates a total of 10 inverters. The inverter values previously derived are briefly summarized in table 7 below.

PV System		Data Origin
Modules per String	17	Equation 9.5
Power per String	9,350 W	Equation 9.6
Strings per Inverter	8	Equation 9.7
Modules per Inverter	136	Equation 9.8
Total Inverters	10	Equation 9.9

Table 7: PV System Inverter Specifications

PV Electrical System Design

Conductors:

PV input to inverter from stings:

The National Electrical Code (NEC), specifically Article 690 and Section 310, will be used to determine the appropriate wire size. As illustrated earlier, each string produces a short circuit current of 14 amps. The DC photovoltaic brief circuit current must be increased by a factor of 1.25 in accordance with NEC 690.8(A)(1). Consequently, to ascertain the DC conductor’s ampacity for the PV system, the short circuit current must be multiplied by Isc*1.25, as illustrated in equation 10.

$ \text{Ampacity} = 11.77A*1.25=14.71A \ \text{(Equation 10)} $

The geographical position of Puerto Rico produces diverse weather conditions, given that the island is near the equator. Therefore, the insulation for wiring will be THWN, which is specifically engineered for both dry and wet conditions with copper conductors. Consequently, figure 10.1 indicates a #14 AWG (THWN) wire, based on the computed ampacity. Nevertheless, to address safety concerns and avoid voltage loss, a #10 AWG (THWN) wire will be selected in place of a #14 AWG (THWN).

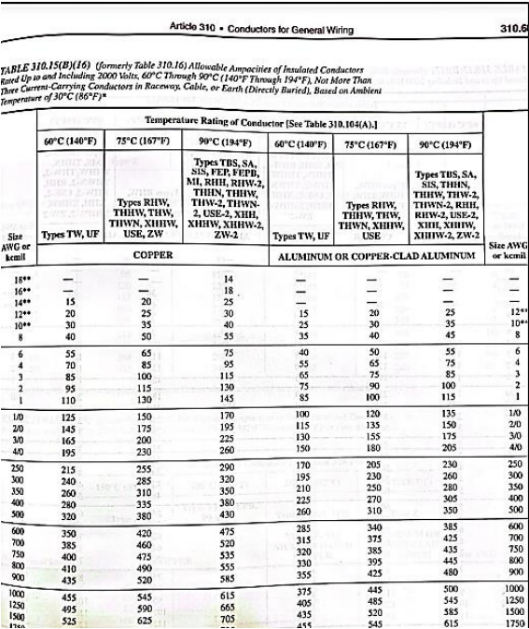
Figure 7: NEC Table 310.15(B)(16)

Inverter to the sub-panel:

The AC output of each inverter will be connected to an AC load sub-panel. The purpose of these sub-panels is to consolidate the individual AC outputs of all inverters into a single AC output that will be directed to the AC main panel. The minimum conductor dimension must have an allowable ampacity that is not less than the non-continuous load plus 125% of the continuous load to calculate the proper AC conductor ampacity, as stated in NEC Article 210.19(A)(1). The selected inverter has a maximum AC output current as illustrated in table 8. The appropriate conductor ampacity required from the inverter to the sub-panel is illustrated in equation 11.

Maximum Output Current

79.5 A

Table 8: Maximum Current at the output

$ \text{Ampacity} = 79.5*1.25=99.37A \ \text{(Equation 11)} $

Ampacity = 79.5 A * 1.25 = 99.37 A: (Equation 11)

Therefore, in accordance with figure 7, a #3 AWG (THWN) size wire is necessary for calculated ampacity. However, a #2 AWG (THWN) size wire will be employed due to safety and voltage drop concerns.

From sub-panels to the primary panel of the substation:

The sub-panels will be divided into three sub-panels. Sub-panels A and B will each contain 5 and 4 inverters respectively, while C will contain only 1. The maximum AC output current for sub-panels A, B and C will be illustrated in table 9. Respectively, based on the maximum inverter current as demonstrated above. According to NEC Article 210.19(A)(1), the minimum conductor size must have an allowable ampacity that is not less than the non-continuous load plus 125% of the continuous load for it to calculate the appropriate AC conductor ampacity. Equations 12, 13, and 14 will be employed to determine the required ampacity for sub-panels A, B, and C.

AC Output Current for Sub-panel A with 5 Inverters	400 A
AC Output Current for Sub-panel B with 4 Inverters	320 A
AC Output Current for Sub-panel C with 1 Inverter	80 A

Table 9: AC Output Current for Inverters

$ \text{Ampacity}_{{sub-panel}_{A}} = 400A*1.25=500A \ \text{(Equation 12)} $
$ \text{Ampacity}_{{sub-panel}_{B}} = 320A*1.25=400A \ \text{(Equation 13)} $
$ \text{Ampacity}_{{sub-panel}_{C}} = 80A*1.25=100A \ \text{(Equation 14)} $

Therefore, in accordance with figure 7, a #500 Kcmil (THWN) size wire is necessary to achieve the calculated ampacity for sub-panels A and B. A #2/0 AWG (THWN) size wire is necessary for sub-panel C to meet the calculated ampacity. Nevertheless, the highest gauge wire that is recommended is #500 Kcmil (THWN) for the sake of simplicity of installation and voltage loss considerations. As a result, a parallel wire run will be implemented to decrease the ampacity necessary for sub-panels A and B.

Junction Box:

Junction Boxes, as depicted in figure 8, are typically constructed from PVC material, and can be installed either grounded or ungrounded. Furthermore, these boxes serve as junctions where electrical wires are merged or introduced to continue their journey through a conduit. Evertec’s PV system comprises 10 inverters with 8 strings, each of which contains 17 PV modules. As a result, 25 junction boxes measuring 8 inches by 8 inches by 4 inches are required, with each box capable of accommodating 17 modules. The cables from the PV modules will be connected to a 20A fuse within these receptacles for overcurrent protection (see section 10.3) prior to being directed to the input of the inverter’s Maximum Power Point (MPP) tracking system.

Figure 8: Junction Box 8’ x 8’ x 4”

Referring to figure 9, the conductor size calculations and NEC table C.10 will be employed to determine the appropriate conduit sizes. The appropriate grounding wire size will be determined by referring to NEC Table 250.66 (see figure 10). PVC Schedule 40 was chosen as the material for all conduits.

Figure 9: NEC Table C.10

Figure 10: NEC Table 250.66

String to Inverter:

Total number of wires = 3
1 positive #10 AWG wire
1 negative #10 AWG wire
1 ground #10 AWG wire
Conduit size = ¾ inch
Total number of conduits = 108

Inverter to Sub-panels:

Total number of wires = 5
3 live #2 AWG wire
1 neutral #2 AWG wire
1 ground #8 AWG wire
Total number of conduits = 4
Conduit size = 3½ inch

Sub-panel A to Substation Main Panel:

Total number of wires = 5
3 live #500 Kcmil wire
1 neutral #500 Kcmil wire
Conduit size = 3½ inch
1 ground #1/0 AWG wire
Total number of conduits = 2 (Parallel wire run)

Sub-panel B to Substation Main Panel:

Total number of wires = 5
3 live #500 Kcmil wire
1 neutral #500 Kcmil wire
1 ground #1/0 AWG wire
Conduit size = 3½ inch
Total number of conduits = 2 (Parallel wire run)

Sub-panel C to Substation Main Panel:

Total number of wires = 5
3 live #2/0 AWG wire
1 neutral #2/0 AWG wire
1 ground #4 AWG wire
Conduit size = 2 inch
Total number of conduits = 1

In an effort to prevent electrocution of responders in the event of a conflagration during daylight, the National Electric Code (NEC) mandates that a rapid shutoff device be connected to each PV module (article 690.12(A) through (B). The sole exception to this code is when the voltage of the PV array is less than 80V. The primary objective of a rapid shutoff switch is to rapidly halt the flow of DC power from individual solar modules and deactivate the entire PV system, even when the sun is still beaming. This is essential for the safety of firefighters during emergencies. This is especially crucial when employing string inverters, as the DC wiring from the solar panels remains energized even when disconnected from the rest of the system in the absence of rapid shutoff switches, which poses a safety hazard. The JMS-F rapid shutoff switch (figure 11) will be installed on the aluminum frame of each PV module for this project. A black cable is utilized to connect the output connector of each module to the input connector of the JMS-F. Red cables are used to connect the output connectors of adjacent JMS-F switches within each string. The 80V limit specified by the NEC is exceeded by the sequences of modules in this proposed system. It is for this reason that JMS-F shutoff devices will be installed on every inverter.

Figure 11: SunSpe model JMS-F Rapid Shutdown System

Protection from Overcurrent:

Conductor ampacity calculations must incorporate a factor of 125% of the maximum current of the PV system, as stipulated in NEC Article 690.8 (A)(1). DC breakers or fuses must be rated for a minimum of 125% of the ampacity determined in NEC Article 690.8(A)(1), as per NEC Article 690.9 (B)(1). Therefore, to guarantee that the system is adequately safeguarded, the subsequent total system current calculations were conducted with a total factor of 156%.

PV Module Short Circuit Current	Data Origin
14 A	Table 9.3

Table 10: Short Circuit Current

String to Inverter:

$ I_{string} = I_{SC}*1.56=14*1.56=21.84A \ \text{(Equation 15)} $

Where:

$ I_{string} = \text{PV string ampacity} $
$ I_{SC} = \text{PV module short circuit current} $

AC breakers or fuses must be rated for a minimum allowable ampacity that is not less than the non-continuous load plus 125% of the continuous load, as per NEC Article 210.19(A)(1). For the purpose of preventing the occurrence of superfluous breaker trips, the appropriate AC triple pole breaker diameters will be determined using the following equations 16 to 20.

Inverter Output Current

79.5A

Table 11: Inverter Current Data

Inverter to AC sub-panel:

$ I_{\text{Max Inverter}} = I_{inv}*1.25=79.5A*1.25=99.37A \ \text{(Equation 16)} $

Where:

$ I_{\text{Max Inverter}} = \text{Inverter ampacity} $
$ I_{inv} = \text{Inverter output current} $

AC sub-panel A to AC main panel:

$ I_{\text{Sub Panel}_{A}} = I_{inv}*Q_{inv}*1.25=99.37A*5=500A \ \text{(Equation 17)} $

Where:

$ I_{\text{Sub Panel}_{A}} = \text{Subpanel A ampacity} $
$ I_{inv} = \text{Inverter output current} $
$ Q_{inv} = \text{Total number of inverters per subpanel} $

AC sub-panel B to AC main panel:

$ I_{\text{Sub Panel}_{B}} = I_{inv}*Q_{inv}*1.25=99.37A*4=400A \ \text{(Equation 18)} $

Where:

$ I_{\text{Sub Panel}_{B}} = \text{Subpanel B ampacity} $
$ I_{inv} = \text{Inverter output current} $
$ Q_{inv} = \text{Total number of inverters per subpanel} $

AC sub-panel C to AC main panel:

$ I_{\text{Sub Panel}_{C}} = I_{inv}*Q_{inv}*1.25=99.37A*1=100A \ \text{(Equation 19)} $

Where:

$ I_{\text{Sub Panel}_{C}} = \text{Subpanel C ampacity} $
$ I_{inv} = \text{Inverter output current} $
$ Q_{inv} = \text{Total number of inverters per subpanel} $

Substation AC main panel:

$ I_{\text{Main Panel}} = I_{inv}*Q_{T}*1.25=99.37A*10=1000A \ \text{(Equation 20)} $

Where:

$ I_{\text{Sub Panel}_{C}} = \text{Subpanel C ampacity} $
$ I_{inv} = \text{Inverter output current} $
$ Q_{inv} = \text{Total number of inverters per subpanel} $

In addition, it is imperative to install a 20A fuse for each PV string and a 100A triple pole breaker to connect the inverter to the AC load sub-panel, as per equations 15 and 16. A 500A main breaker is necessary to connect 5 inverters to sub-panels A, 4 inverters to sub-panel B with a 400A main breaker, and 1 inverter to subpanel C with a 100A main breaker, as illustrated in equations 17, 18 and 19. For the protection of the AC main panel at the substation, a 1000A main breaker will be installed, as illustrated in equation 20. In the event of an overcharge or short circuit, these breakers and fuses are designed to protect the system. Table 12 provides a summary of the overcurrent protection devices.

Protection	Triple Pole Breaker	Fuse
PV strings to inverter	N/A	20A
Inverter to AC sub-panel	100A	N/A
AC sub-panel A to AC main panel	500A	N/A
AC sub-panel B to AC main panel	400A	N/A
AC sub-panel C to AC main panel	100A	N/A
Substation AC main panel	1000A	N/A

Table 12: Overcurrent protection devices for the PV system

A tolerable voltage drop of 3% is allowed for the most distant receptacle in a branch circuit, according to the National Electrical Code (NEC). Nonetheless, a maximum voltage variation of 5% is allowed when considering the feeders connected to the branch circuit panel. A maximum voltage variation of 3% is allowable for both DC and AC systems due to the load side connector type. The NEC’s tables 8 and 9 will be used for calculating DC and AC voltage drop in this project, respectively, since the utilization of ohms per kilofoot (ohms/kft) for voltage drop assessment.
Furthermore, manual calculations will be performed using specific equations that are designed for both AC and DC systems. In accordance with NEC regulations, the precise determination of voltage drop is guaranteed by Equations 21, 22, and 23:

$ V_{drop_{DC}} = \frac{M*I*L*R}{P} \ \text{(Equation 21)} $

Where:

$ V_{drop_{DC}} = \text{DC voltage drop in volts} $
$ M = \text{Multiplier: 2 for DC voltage drop} $
$ I = \text{Current in amps} $
$ L = \text{Length of conductor} $
$ R = \text{Resistance in ohms/kFT} $
$ P = \text{Parallel wire runs} $

$ V_{drop_{AC}} = \frac{M*I*L*R}{P} \ \text{(Equation 22)} $

Where:

$ V_{drop_{AC}} = \text{AC voltage drop in volts} $
$ M = \text{Multiplier: } \sqrt{3} \text{ for DC voltage drop} $
$ I = \text{Current in amps} $
$ L = \text{Length of conductor} $
$ R = \text{Resistance in ohms/kFT} $
$ P = \text{Parallel wire runs} $

$ \text{%}V_{drop} = \frac{V_{drop}}{V_{L-L}}*100 \ \text{(Equation 23)} $

Where:

$ \text{%}V_{drop} = \text{Percentage of voltage drop} $
$ V_{drop} = \text{Voltage drop in volts} $
$ V_{L-L} = \text{Line voltage} $

DC Voltage Drop:

An Excel spreadsheet tool was developed using equations 21 and 23 to compute and recommend the suitable conductor size for the PV system based on DC voltage loss.

DC Voltage Drop
Multi-Level Parking
Distance (ft)	613.80
Wire Gauge	10 AWG
Wire Resistance(ohm/kft)	1.24
Wire Runs	1
Voltage Drop (V)	13.37
%Vdrop	1.59%

Ground-Level Parking
Distance (ft)	478
Wire Gauge	10 AWG
Wire Resistance(ohm/kft)	1.24
Wire Runs	1
Voltage Drop (V)	10.41
%Vdrop	1.23%

Table 13: DC Voltage Drop Calculation Results.

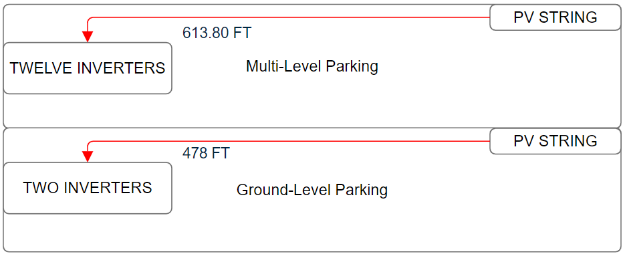
Figure 12: Longest Distance measurement of Multi-Level and Ground-Level Parking for DC voltage drop calculation.

AC Voltage Drop:

The distance from the inverters to the AC sub-panels A, B, and C may be considered negligible owing to their closeness. Consequently, the AC voltage loss will be exclusively assessed for the wire route from the AC sub-panels A, B, and C to the main panel of the AC substation

AC Voltage Drop
Multi-Level Parking
Distance (ft)	868.9
Wire Gauge	500 Kcmil
Wire Resistance(ohm/kft)	0.0258
Wire Runs	4
Voltage Drop (V)	3.86
%Vdrop	0.80%
Ground-Level Parking
Distance (ft)	468.2
Wire Gauge	2/0 AWG
Wire Resistance(ohm/kft)	0.0967
Wire Runs	1
Voltage Drop (V)	6.23
%Vdrop	1.30%

Table 14: AC Voltage Drop Calculation

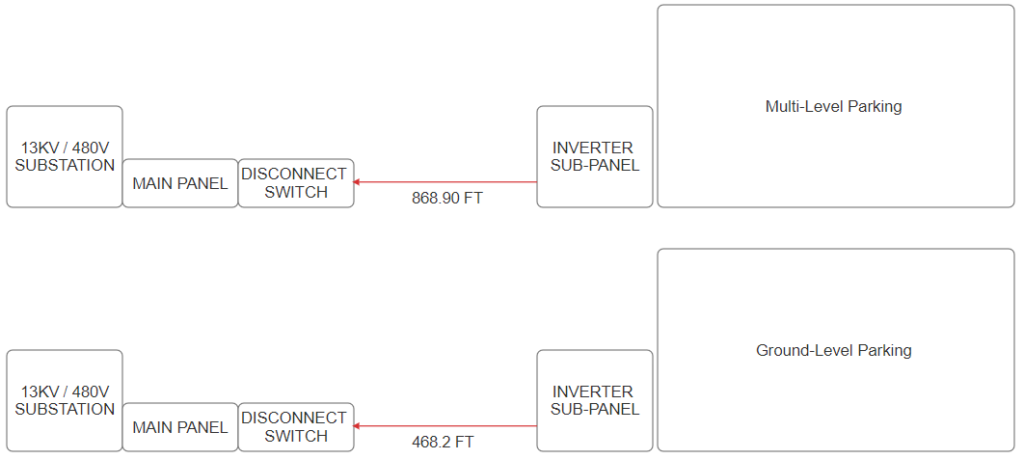
Figure 13: Longest Distance measurements of Multi-Level and Ground-Level Parking for AC voltage drop calculation.

PV Civil System Design

A carport is a covered structure that is employed to provide limited protection to vehicles, predominantly automobiles, from the elements such as the sun, rain, and snow. Carports, in contrast to garages, are typically open on one or more sides and may be either freestanding or affixed to a wall. Additionally, carports are available in a variety of materials and designs, including metal, wood, and composite materials, and can be either temporary or permanent structures.

Benefits of Carports:

Cost-effective: In general, it is less expensive to construct and maintain than a completely enclosed garage.
Installation simplicity: The installation of a carport is generally less complex and more efficient than the construction of a garage.
Weather protection: Although carports are not entirely enclosed, the encloser still offers protection from the sun, rain, and precipitation, which can help prolong the lifespan of a vehicle’s interior and paint.
Ventilation: Carports are open-air structures, which facilitate superior ventilation in comparison to garages. This can mitigate the risk of mildew or pollutants.
Versatility: Equally important, carports function as shaded outdoor spaces for activities other than parking vehicles, such as a covered area for barbecues, gatherings, or outdoor storage.

Specifications in accordance with the Puerto Rico Electric Code:

The local building and electrical codes in Puerto Rico require specific considerations when constructing a carport. These codes are in accordance with the National Electrical Code (NEC) but may include specific amendments.

Electrical Wiring and Outlets: The wiring must adhere to the NEC and local amendments if the carport has illumination, outlets, or other electrical installations. This encompasses the utilization of components that are both outdoor-rated and weather-resistant in order to endure the humid and coastal climate. Improving the system’s safety, it is necessary to install Ground Fault Circuit Interrupter (GFCI) protection on all outdoor receptacles.
Lightning Protection: In view of Puerto Rico’s frequent thunderstorms, it may be prudent to evaluate lightning protection for carports with metal structural elements. The structure can be protected by the implementation of lightning rods or grounding mechanisms.
Adherence to Zoning Regulations and Setbacks: The carport must comply with zoning regulations that define the maximum height, coverage limits for impermeable surfaces, and setbacks from property lines.
Wind Load Requirements and Structural Integrity: Carports must be constructed to withstand high wind loads, which can typically reach 165 mph or higher, depending on the location, due to Puerto Rico’s hurricane-prone status. This may entail the utilization of reinforced anchoring systems or heavier materials to ensure the pergola is securely fastened to the earth.

This is optimal for situating the PV system in this endeavor. Section 16.3 of Chapter 16 contains information regarding the materials and prices.

Cogen. Load Analysis

Calculations for the energy produced will be done using the data provided by the manufacturer of the cogeneration plant and Evertec. Firstly, defining energy produced, which refers to the total amount of usable energy generated by the system, typically measured in kilowatt-hours (kWh). This includes the electrical energy output and, where applicable, the thermal energy recovered and used in the system. In a cogeneration system, energy production reflects the generator’s ability to efficiently convert fuel into electricity and heat.

The generator’s maximum wattage is known, and how many loads. Additionally, knowing that 7.43 ft³ of natural gas is required to generate 1 kWh of electricity under standard conditions. This value is based on the energy content of natural gas, which is typically 1,030 BTU/scf, and the conversion ratio 1 kWh = 3,412 BTU.

The energy generated is directly related to the output of the generator, as outlined in equation 24 below. Convert the natural gas flow rate from ft³/h to m³/h to comply with local regulations, then use the energy content of natural gas to compute the equivalent kWh for energy generation. In the absence of precise fuel data, using conventional values for the composition and energy content of natural gas. The conversions and energy content data facilitate the calculation of the generator’s energy output, as seen in equation 25.

$ \text{Energy Consumed} = \text{Max Wattage of Generator}*\text{Loads}*7.43ft^3 \ \text{(Equation 24)} $
$ \text{Energy Consumed} = 1,200kWh*1*7.43ft^3 = 8,916ft^3/h $

$ (\frac{8,916ft^3}{h}) (\frac{1m^3}{35.315ft^3}) = 252.471m^3/h $
$ (\frac{252.471m^3}{h}) (\frac{35.31scf}{1m^3}) = 8,914.75scf/h $

$ \frac{(\frac{8,914.75scf}{h})(\text{Energy Content})}{3,412BTU} = \frac{(\frac{8,914.75scf}{h})(\frac{1,030BTU}{scf})}{3,412BTU} = 2691.15kWh $

Power kW	Energy Produced (scf/h)	Energy Produced (kWh)
1,200	8,914.75	2,691.15

Table 15: Calculations results for energy produced and peak wattage.

Calculations of the electrical energy consumed (EC) are shown below. Additionally, table 15 shows the data sheet for heat exhaust, from the manufacturer, where the calculations are referenced from.

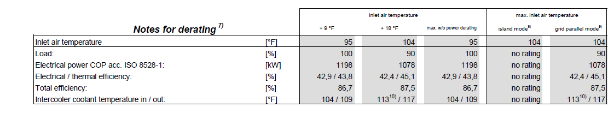
Figure 14: Generator plant datasheet.

The following values are taken from the generators data sheet (figure 14), and with some simple calculations, the values needed for the load analysis can be achieved. The conversion from BTU to kWh can be seen in equation 25 above. Additionally, some values like the enthalpy of feed water and steam enthalpy at 8 BARS were taken from another analysis done in Evertec, by Group 162, and were taken as reference for the analysis.

Exhaust heat with temp. after heat exchanger (Q) = 33,184 BTU/min= 583.63 kW
Exhaust heat with 10% losses = 583.63*90%=525.267 kW
Available heat = 525.267 kW or 525.267 kJ/s
Enthalpy of feed water at 91.84℃ = 385 kJ/kg
Steam Enthalpy at 8 BAR = 2768 kJ/kg
Net enthalpy = (2768 kJ/kg) – (385 kJ/kg) = 2383 kJ/kg

The values obtained from the generator’s data sheet, the next step calculate the steam generated to move the turbine and express it in kg/h. This is done in equation 26, and in equation 27, the conversion to kW was made.

$ \text{Steam generated}(m) = \frac{\frac{kJ}{s}}{\frac{kJ}{kg}} = \frac{\frac{525.267kJ}{s}}{\frac{2383kJ}{kg}} = \frac{0.22kg}{s} = 792kg/h \ \text{(Equation 26)} $
$ m = \frac{steam*\text{net entahlpy}}{3,600s} = \frac{(\frac{792kg}{h})(2383kJ/kg)}{3600s} = 524kW \ \text{(Equation 27)} $

Below, in table 16, are the results for the steam generated. The weekly average peak wattage of Evertec was taken from the 2024 electrical bills, where an average of 9 months since the data was collected from January to September of 2024 (actual).

Average Peak Production (kW)	839.388
Available heat (kW)	525.267
Inlet water temperature (℃)	93
Generated steam (kg/h)	792
Steam (kW)	524

Table 16: Results for the generated steam.

Now the calculations of the hot water and steam generation for chillers.

Figure 16: Cooling system data sheet.

The following data is taken from the cooling system data sheet (figure 16). As a result of steam being in units of m³/h, the necessary conversion was made to change the units to m³/h. After this, an additional conversion must be made to change the units into kg/h, and this is done by multiplying the water flow rate by the density of water which is 1,000 kg/m³. Computation gives the mass flow rate of water, and this is done below in equation 28. Finally, in equation 29, the next step is to calculate the change in temperature of water in optimal conditions, and as mentioned before, these values were taken as reference from Group 162, who already made the analysis on Evertec.

Hot water flow rate = 38 m³/h
Specific Heat of Water = 4.2 kJ/kg

$ \text{Steam}(m) = (38m^3/h)(1,000kg/m^3) = 38,000kg/h \ \text{(Equation 28)}$
$ \text{Delta T} = \text{Inlet Temp} – \text{Outlet Temp} = 93^\circ C – 80^\circ C = 13^\circ C \ \text{(Equation 29)} $

The formula that expresses the quantitative relationship between heat transfer and temperature change includes three key factors: Q = mcΔT, where Q represents the heat transfer, m is the specific energy needed to increase 1kg of the substance by 1℃, c is the specific heat of water, and ΔT is the change in temperature. This calculation is done in equation 30 and gives the hot water generated in kJ/s, which is kWh too. Lastly, calculating the hot water consumption by using a specific heat for water at 4,186 J/kg ℃, and the process is shown in equation 31.

$ Q = \frac{mc*\text{Delta T}}{3,600s} = \frac{38,000kJ/h * 4.2kJ/kg * 13^\circ C}{3,6000s} = 576.33kJ/s \ \text{(Equation 30)} $
$ Q = \frac{576.33kJ}{s} = 576.33kWh $
$ m = \frac{Q}{c * \text{Delta T}} = \frac{576.33kW}{4,186 \frac{J}{kg} ^\circ C * 13^\circ C} = 10.59kg/s \ \text{(Equation 31)} $

A summary of all data collected and calculated for the load analysis is on table 17 below.

Power (kW)	1,200
Energy Production (scf/h)	8,916
Energy Production (kWh)	2,691.147
Average Peak Production (kW)	839.388
Available heat (kJ/s)	524.7
Inlet Max temperature (℃)	93
Generated Steam (kg/h)	792
Steam (kW)	524
Hot Water Flow Rate (kg/h)	38,000
Change in temperature (℃)	13
Specific Heat of Water (kJ/kg)	4.2
Hot Water Generated (kWh)	576.33
Hot Water Consumption (kg/s)	10.59

Table 17: Summary of all calculations.

The data collected highlights the system’s high efficiency in utilizing energy to generate heat and steam. With a substantial power output of 1,200 kW, the energy produced is approximately 2,691.15 kWh, reflecting effective energy conversion from the supplied fuel. A consistent weekly average power output of approximately 839.39 kW further demonstrates stable and reliable performance over time. The system effectively harnesses available heat, producing a heat output of 524.7 kJ/s, which contributes to a steam generation rate of 792 kg/h and a corresponding steam power output of 524 kW. Additionally, the hot water flow rate of 38,000 kg/h with an inlet temperature of 93°C and a temperature differential of 13°C highlights the system’s capacity to deliver hot water at a significant rate. By leveraging the specific heat of water (4.2 kJ/kg·°C) and a hot water consumption rate of 10.59 kg/s, the system demonstrates exceptional efficiency in thermal energy delivery. The energy produced is indicative of the system’s overall performance in converting fuel into both electrical and thermal outputs. Overall, the data confirms that the system performs with a high degree of efficiency in energy production and heat utilization, making it a robust solution for cogeneration applications.

Cogen. Performance Analysis

In the power plant industry, combined heat and power technology stand out for its high thermodynamic efficiency. Cogeneration plants, designed to challenge traditional methods, focus on maximizing both power output and overall efficiency of the systems where it is installed. Unlike conventional power plants, cogeneration plants generate electricity and capture useful thermal energy from a single fuel source simultaneously. A cogeneration plant’s main goal is to enhance efficiency by producing electricity and effectively utilize the heat waste generated by the fuel source. In a combined heat and power (CHP) system, the focus is on delivering multiple benefits, including electricity generation, and supplying useful heat tailored to meet the needs of end users in the way of refrigeration or heating. This client-focused approach offers a more efficient, sustainable, and adaptable power generation solution; by capturing waste heat, cogeneration systems can reach an efficiency of 60 to 80 percent, significantly higher than traditional methods. This improvement is especially noticeable when using natural gas, as it requires less fuel and leads to lower costs compared to buying electricity separately.

Evaluating the theoretical efficiency for the cogeneration plant when it is running at 100 %

Electrical Efficiency – NELEC is described as the “Net Electrical Efficiency,” and it is the ratio between the output electrical useful energy (EC) and the input fuel power (FC). In table 15, the values for peak energy and energy consumed are present.

Data	Value
Peak Energy (Output)	1,200 kW
Energy Produced (Input)	2,691.147 kWh

Table 18: Data Values from Load Analysis for Electrical Efficiency

$ \text{Net Electrical Efficiency} = \frac{\text{Energy Consumed}}{\text{Energy Produced}} * 100 \ \text{(Equation 32)} $
$ \text{Net Electrical Efficiency} = \frac{1,200kW}{2691.147kWh} * 100 = 44.59\% $

The NELEC system is a measure of how effectively it converts fuel energy into useful electrical energy. Used the typical efficiency formula, the system’s output figure by the input of said system. This case, the output is the electrical energy consumed by the load and the input is the fuel energy injected into the plant. An electrical efficiency of 44.59% of what the generator produces. This means that the system can convert approximately 44.59% of the total energy injected into useful electrical energy. A higher NELEC efficiency rating indicates a more efficient system, as it can produce more electricity with the same amount of fuel injected into the system.

Mechanical Efficiency – Mechanical efficiency in a cogeneration plant refers to the effectiveness with which the plant converts the input energy from fuel into useful mechanical work, typically to drive turbines or generators. In cogeneration, the goal is to maximize this efficiency by utilizing both the mechanical power for electricity generation and the waste heat for heating or other processes. This dual-use approach improves the overall energy efficiency of the cogeneration plant compared to traditional power plants. Mechanical efficiency in a cogeneration system is influenced by factors like the quality of fuel, turbine performance, and the integration of heat recovery systems. Finally, by optimizing mechanical efficiency, cogeneration plants achieve higher energy output with reduced fuel consumption, resulting in economic savings and a lower environmental impact. This calculation is done in equation 25.

Data	Value
Steam Generated (Output)	524 kWh
Energy Produced (Input)	2,691.147 kWh

Table 19: Data Values from Load Analysis for Mechanical Efficiency

As can be seen in equation 3, the mechanical efficiency for the system is approximately 19.47%. This means that the cogeneration plant utilizes 19.47% of the fuel injected as steam, effectively. This is used to drive the steam turbine and move the generator.

$ \text{Mechanical Efficiency} = \frac{\text{Steam Generated}}{\text{Energy Produced}} * 100 \ \text{(Equation 33)} $
$ \text{Mechanical Efficiency} = \frac{524kWh}{2,691.147kWh} * 100 = 19.47\% $

Hot Water Efficiency – Hot water efficiency in a cogeneration plant refers to the effective utilization of waste heat to produce hot water for heating or industrial processes, maximizing overall system efficiency. In a cogeneration setup, the plant generates electricity, and the excess heat that would otherwise be lost is captured and used to heat water. This hot water can then be distributed for building heating, domestic hot water, or other industrial uses. By effectively using this thermal energy, cogeneration plants reduce the need for additional energy sources to heat water, increasing the plant’s overall energy efficiency. This not only lowers fuel consumption, but reduces operating costs and the environmental impact, making the plant more sustainable and economical in the long term. The computation for the hot water efficiency is done below, in equation n.

Data	Value
Hot Water Generated (Output)	576.33 kWh
Energy Produced (Input)	2,691.147 kWh

Table 20: Data Values from Load Analysis for Hot Water Efficiency

$ \text{Hot Water Efficiency} = \frac{\text{Hot Water Generated}}{\text{Energy Produced}} * 100 \ \text{(Equation 34)} $
$ \text{Hot Water Efficiency} = \frac{576.33kWh}{2,691.147kWh} * 100 = 21.41\% $

The hot water efficiency of a system measures how effectively it converts fuel energy into hot water. The system can convert approximately 21.41% of the input fuel energy into hot water. Higher hot water efficiency indicates a more efficient system in terms of producing hot water for industrial processes or facilities. Finally, the overall efficiency of the cogeneration plant system is the sum of all efficiencies, which is done below, in equation 35.

$ \text{Overall Heat Efficiency} = \text{Elec. Eff.} + \text{Mech. Eff.} + \text{Hot Water Eff.} \ \text{(Equation 35)} $
$ \text{Overall Heat Efficiency} = 44.59\% + 19.47\% + 21.41\% = 85.47\% $

In summary, the efficiencies provided for the performance of the cogeneration plant details its ability to convert input fuel into effective energy usage. Based on the calculations done, the maximum overall efficiency of the system is 85.47%, meaning that the system is effectively utilizing most of the available energy to produce power, and can be compared to the efficiency of the manufacturer’s data sheet. Additionally, these values are close to each other, meaning that there is proof that the value calculated is correct, and this can be observed below, in figure 17. Finally, table 21 highlights every efficiency calculated.

Figure 17: Generator Data Sheet.

Electrical Efficiency (%)	Mechanical Efficiency (%)	Hot Water Efficiency (%)	Overall Efficiency (%)
44.59	19.47	21.41 %21.41 %	85.47

Table 21: Efficiency Results.

Economic Billing Assessment

Starting the Cost analysis and economic consumption of the pre-cogeneration, a careful observation at Table 22 below it has to made, because it will be the standard for this analysis. This table shows the data taken from the electric bills. In addition, it provides a detailed comparison of the energy consumption and cost for 2019 and 2020, before the installation of the cogeneration system at the Cupey Center Buildings. In context, the calculated values were the average ones, which were made by taking the data given from Evertec and dividing it each year by all the months (12), for the energy consumption and cost.

Year	2019	2020
Total Energy (kWh)	11,515,898	11,079,377
Average Energy (kWh)	959,658	923,281
Total Cost ($)	2,329,939	194,161
Average Cost ($)	2,116,091	176,340

Table 22: Energy Consumption and Cost Comparison Before COGEN Installation

In 2019, the buildings recorded an average monthly energy consumption of 959,658.17 kWh and an average monthly cost of $194,161.62. The high energy usage and associated costs highlight the building’s significant operational demands during this period. In 2020, the building’s average monthly energy consumption decreased to 923,281.48 kWh, and the average monthly cost dropped to $176,340.97. While there was a reduction in both energy usage and costs, the building continued to face substantial energy expenditures, indicating that efficiency measures had yet to be implemented.

In summary, 2020 reflects improved energy management compared to 2019, with stable energy consumption and reduced costs. This serves as a baseline for comparing the financial and operational impacts after the installation of the cogeneration system.

Now for the post-cogeneration energy consumption and cost evaluation, the standard for this analysis is in table 23, and 24, which has calculated average values and other data given by Evertec. Therefore, this table presents the energy consumption from the electric utility and cost data for 2021 to 2024, following the installation of the COGEN system at the Cupey Center Buildings. The significant reduction in energy consumption from the electric utility is directly attributable to the COGEN system, which allowed the building to meet much of its energy needs internally.

Year	Total Energy (kWh)	Average Energy (kWh)
2021	3,554,410.00	296,200.83
2022	2,789,160.00	232,430.00
2023	1,081,080.00	90,090.00
2024	856,680.00	95,186.67

Table 23: Energy Consumption Analysis After COGEN Installation

Total Cost ($)	Average Cost ($)
797,229.16	66,435.76
925,275.77	77,106.31
407,919.12	33,993.26
309,732.38	34,414.71

Table 24: Energy Cost Analysis After COGEN Installation

In 2021, following the COGEN system’s implementation, there was a sharp decrease in average monthly energy consumption from the electric utility to 296,200.83 kWh. Along with this reduction, the average monthly cost fell to $66,435.76. This decrease in reliance on external electricity is due to the COGEN system generating a substantial portion of the buildings’ power needs internally. The significant drop in both utility-supplied energy consumption and costs highlights the immediate impact of the COGEN system’s integration.

In 2022, total energy consumption from the electric utility decreased further to 2,789,160 kWh, with an average monthly usage of 232,430 kWh. However, the total cost increased to $925,275.77, with an average monthly cost of $77,106.31. This rise in costs, despite reduced energy consumption, is likely to reflect the transition to full operational use of the COGEN system, as well as possible changes in energy rates. The building’s reliance on external power continued to decrease, but fluctuations in energy pricing led to an increase in expenses.

Subsequently, in 2023 the downward trend in utility energy consumption continued, reaching 1,081,080 kWh, with an average monthly usage of 90,090 kWh. The total cost for energy dropped significantly to $407,919.12, resulting in an average monthly cost of $33,993.26. This reduction in both energy consumption and costs reflects improved efficiency of the COGEN system, which enabled the building to further reduce its dependence on external electricity. The system’s increasing efficiency helped lower costs, possibly aided by better operational practices and more efficient energy management.

Now in 2024, the buildings’ average monthly energy consumption from the electric utility rose a little at 95,186.67.14 kWh, with an average monthly cost of $34,414.71, keeping in mind this average may lower as the year passes. This continued reduction in energy consumption and costs indicates the ongoing optimization of the COGEN system, allowing the building to minimize its use of external power. The data shows the system’s long-term benefits in reducing utility energy consumption.

The data from 2021 to 2024 reflects the building’s transition to a more self-sustained energy model, with the COGEN system dramatically reducing the need for external electricity. While energy consumption from the electric utility has steadily decreased, costs have fluctuated, likely influenced by changes in energy rates and external market factors. Overall, the COGEN system has led to a more cost-effective and efficient energy consumption model, as the buildings’ reliance on the electric utility diminished significantly.

The implementation of the cogeneration (COGEN) system at the Cupey Center Buildings, along with the integration of chillers within the combined heat and power (CHP) system, resulted in a notable increase in water consumption and related costs demonstrated in table 25.

Metric	Before COGEN	After COGEN	Change
Ave. Monthly Volume	2,218.58 (m^3)	2,738.73 (m^3)	520.15 (m^3)
Ave. Yearly Volume	26,623.00 (m^3)	32,864.80 (m^3)	6,241.80 (m^3)
Ave. Monthly Cost	$15,067.10	$19,715.86	$4,648.76
Ave. Yearly Cost	$180,805.21	$236,590.28	$55,785.08

Table 25: Water Consumption and Cost Breakdown for 2020 and 2021

Before the COGEN system, the building consumed an average of 2,218.58 m³ of water per month. However, after the installation of the system and the use of chillers, the consumption increased to 2,738.73 m³ per month, representing an increase of 520.15 m³. Annually, this increase in water usage rose from 26,623.00 m³ to 32,864.80 m³, with an additional consumption of 6,241.80 m³ each year.

This rise in water consumption was accompanied by an increase in costs. Before the COGEN system was implemented, the average monthly water cost was $15,067.10. After the system became operational, the average monthly cost increased to $19,715.86, reflecting an additional cost of $4,648.76 per month. On a yearly basis, the water costs rose from $180,805.21 to $236,590.28, a total increase of $55,785.08.

The increase in water consumption and costs can be directly attributed to the operational demands of the chillers, which require additional water as part of the cooling process. While the COGEN system effectively reduced the building’s reliance on external electricity and helped lower electricity costs, the use of chillers has introduced new operational expenses. This increased demand for water is expected in CHP systems that use absorption chillers to enhance efficiency, but it reflects the trade-offs in resource use associated with such systems.

Subsequently, the COGEN system has successfully reduced electricity consumption and operational costs, the integration of chillers within the CHP system has led to a significant rise in water consumption and costs. This increase highlights the complex balance between improved energy generation efficiency and the additional resources required for system cooling. As the system continues to optimize energy use, the ongoing management of water resources will play a key role in maintaining overall operational efficiency.

Building upon previous research, Table 26 shows the calculated and given data. This table compares the energy consumption and costs, before and after the installation of the COGEN system. The installation of the COGEN system at the Cupey Center Buildings resulted in a significant reduction in the energy consumption sourced from the electric utility. From 2019 to 2020, the building relied entirely on external power provided by the utility company. During this period, the average monthly energy consumption from the electric utility was 941,469.83 kWh, with an average monthly cost of $185,251.29. These figures highlight the substantial energy demand of the building, and the associated excessive costs reflect the reliance on external energy supply, which can be subject to fluctuating market prices.

Metric	Before COGEN	After COGEN	Savings (%)
Average Monthly Energy (kWh)	902,022.00	184,029.56	79.60
Average Yearly Energy (kWh)	10,824,264.00	2,208,354.67	79.60
Average Monthly Cost ($)	175,685.59	54,225.70	69.13
Average Yearly Cost ($)	2,108,227.13	650,708.38	69.13

Table 26: Comparative Analysis of Pre and Post COGEN Energy and Costs

Furthermore, with the installation of the COGEN system, the energy profile of the building shifted significantly. From 2021 to 2024, the average monthly energy consumption from the electric utility decreased dramatically to 180,582.60 kWh, reflecting a reduction of 760,887.23 kWh compared to the pre-COGEN period. This decrease represents an 80.82% reduction in the building’s dependency on the external power grid. Along with this reduction in energy consumption, there was a substantial decrease in costs, with the average monthly cost falling to $53,368.21, saving the building $131,883.08 per month on utility bills, which equates to a 71.19% reduction in costs.

The dramatic reduction in energy consumption from the electric utility after the COGEN system was implemented underscores the system’s ability to meet a substantial portion of the building’s energy needs internally. The system allowed the building to reduce its reliance on external power, thereby lowering operational costs. The sharp decline in average monthly utility costs signifies the economic efficiency of the COGEN system, contributing to considerable long-term savings.

Comparing energy consumption and costs before and after the installation of the COGEN system, the system has had a transformative impact on the building’s energy management. The substantial decrease in utility-sourced energy, along with the significant reduction in associated costs, reflects the effectiveness of the COGEN system in optimizing the building’s energy efficiency. This transition to internal energy generation has not only reduced the buildings’ dependency on the electric utility but demonstrated the financial viability of cogeneration technology for long-term operational savings.

Microgrid System Simulations

Helioscope is a photovoltaic system simulator created by Folsom Labs in San Francisco, available by subscription, specifically intended for creating PV system pictures at the client’s designated site. Helioscope’s advanced modelling capabilities evaluate the system’s performance under various conditions, ensuring maximum efficiency. The cloud-based platform utilizes a systematic process that begins with the input of project details, such as location, roof characteristics, and specific system requirements, enabling the assembly of the solar array.

Data including the system’s location, chosen solar panels, and inverters will be entered. Utilizing this information, the specified area will be filled with solar panels until the necessary number of modules and the appropriate inverter capacity are attained. This procedure involves carefully positioning solar panels until the determined amount corresponds with the total power consumption needs. Subsequently, Helioscope will provide the site and relevant information of the solar system, delivering a comprehensive visual report along with a detailed cost-benefit analysis.

Additionally, to start a project in Helioscope, users must adhere to the following procedures. The user must first visit Helioscope.com and choose “New Project.” The project’s name, address, and site classification (commercial, ground-mounted, or residential) must thereafter be recorded. Subsequently, selecting “New Design” followed by “Create New Design” will direct people to the specified URL. Consequently, figure 18 shows that the chosen program was Evertec, located in San Juan, Puerto Rico.

Figure 18: Selected Project Location Evertec

The selected location, as seen in figure 19, is for the carport were identified. This design consists of eight primary carport photovoltaic array sections positioned inside the multi-level parking facility of Evertec, in addition to one smaller part situated in the ground-level parking area.

Figure 19: Photovoltaic Module Areas Evertec

Upon selecting the PV module locations, the necessary input data pertaining to the system was entered, as seen in figure 20. For this photovoltaic system design, the chosen module will be identical to that of the photovoltaic design.

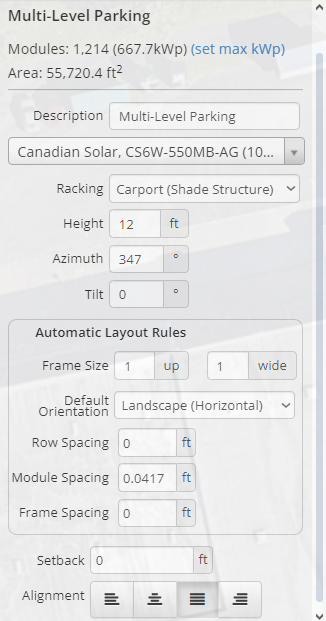
Figure 20: Input Data for Multi-Level Parking

Moreover, figure 21 below illustrates the input data for the AC wiring zone of Parque Central. The PV design for Parque Central will use the same inverter as the CDT design, namely the SMA Sunny Tripower CORE1 62-US.

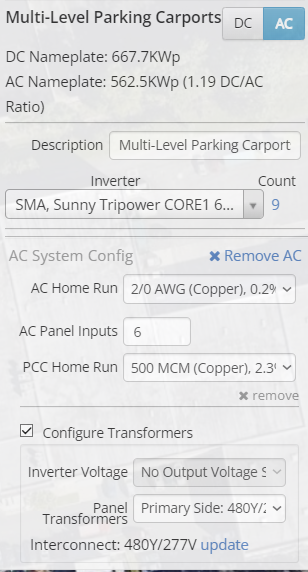
Figure 21: Wiring Zone AC Input Data for Multi-Level Parking

The configuration of the modules for Evertec’s design will be situated on the natatorium’s parking lot. As seen in figure 18, the carport installation consists of eight primary portions inside the multi-level parking and one supplementary section located in the ground-level parking. Eight tiers of the multi-level parking include 1,214 modules, whilst the ground-level parking area will consist of 150 modules. A total of 1364 modules will be present.
Furthermore, as seen in figure 22, and table 27, the Helioscope presents a production graph indicating output exceeding 80 KWh each month throughout the production period. Moreover, producing over 110 kWh in a minimum of three months annually.

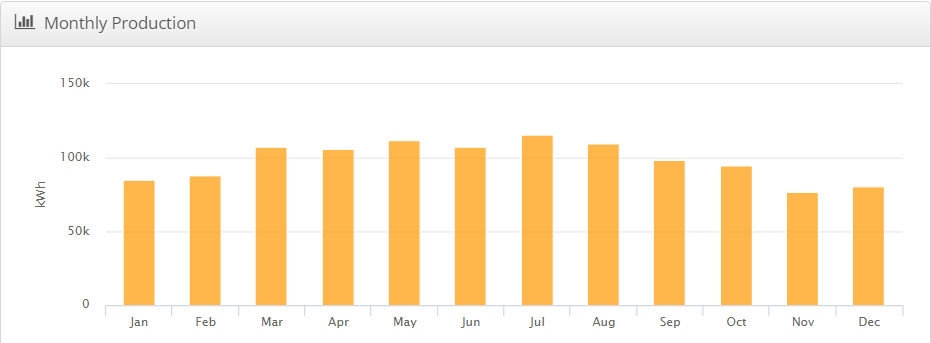
Figure 22: Evertec’s Helioscope Monthly Production Simulation

The total collector irradiance accessible to the modules in the Evertec array was estimated to be 1,813.7 kWh/m². The yearly energy output to the grid was determined to be 1,181,496.6 kWh, as seen in figure 23. Table 27 presents a comprehensive analysis of the monthly AC solar output at Evertec.

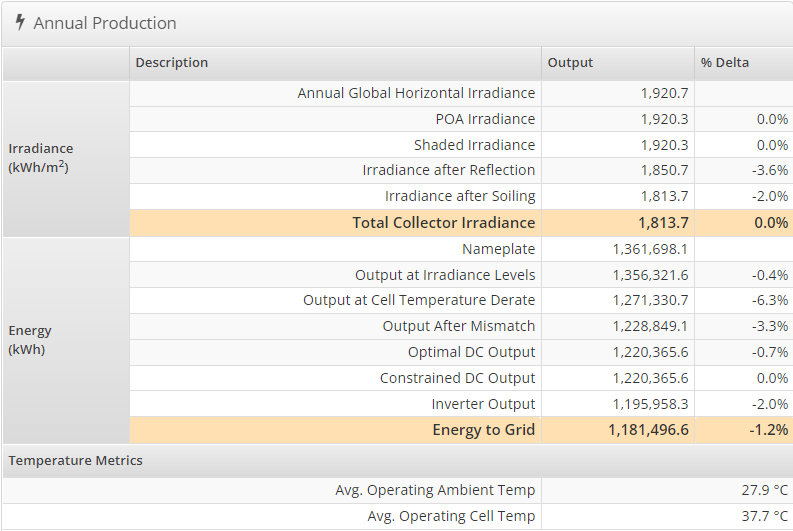
Figure 23: Evertec’s Helioscope Annual Production Simulation

Month	Energy to Grid (KWh)
January	84,737.6
February	88,028.0
March	107,301.0
April	106,253.5
May	111,839.1
June	107,277.1
July	115,399.8
August	110,002.1
September	98,493.7
October	94,679.6
November	76,546.4
December	80,937.2

Table 27: Evertec’s Monthly AC Solar Production

The condition set report for Evertec was furnished, as shown in figure 24. This report delineates all environmental factors that could potentially impact the system’s performance.

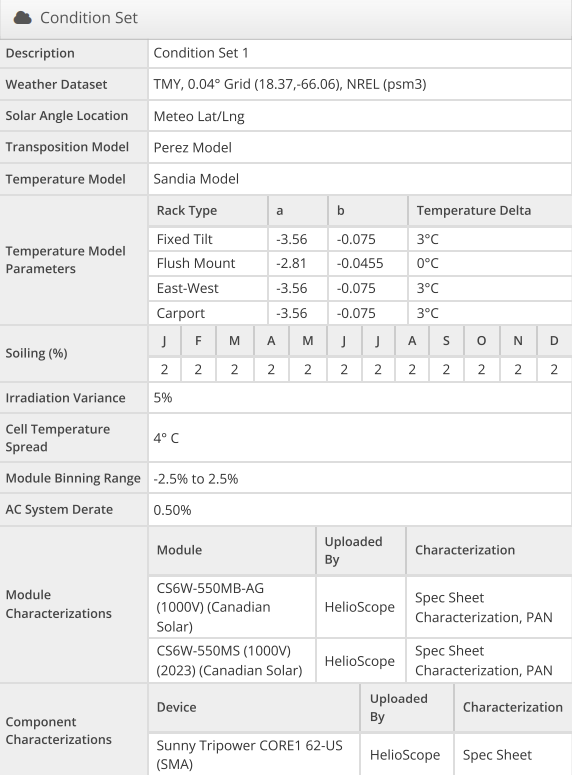
Figure 24: Evertec’s Condition Set

The generating loss, in figure 25, depicts the generating losses where the predominant energy loss is due to temperature, being 6.3% of the total generation. Mismatch losses are 3.3%, reflection loss is 3.6%, and all other losses are at or below 2%, as seen in the graph.

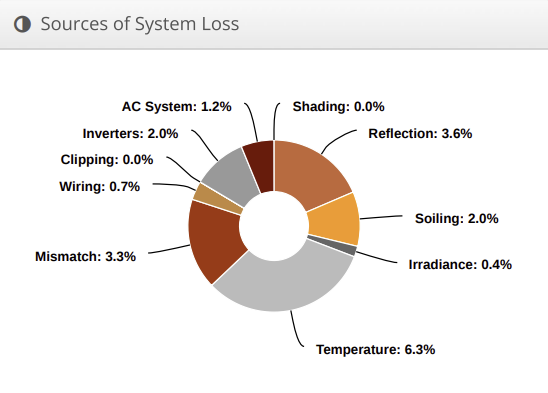
Figure 25: Evertec’s System Loss Simulation

Finally, Helioscope assesses the impact of surrounding shadows on the modules and delivers irradiation percentages accordingly. The design indicates that the irradiation level is minimal, as seen in figure 15.8, owing to the height of the multi-level parking and the absence of vegetation in the ground-level parking. Furthermore, Helioscope provides the system metrics for Evertec’s comprehensive project, which will be shown in figure 26.

The next step is to incorporate the percentage of losses generated by the electric system, which encompasses wiring, shading, connections, light-induced degradation, nameplate rating, availability, soiling, and incompatibilities. The Helioscope simulation was employed to determine these percentages of losses, as illustrated in table 28. The electric system’s calculated loss is in percentage. Consequently, the solar array’s total output power can be calculated by employing equation 36 and the power output considering temperature effects is displayed in table 28.

%Ploss

19.5%

Power output considering temperature effect

735,006 W

Table 28: %Ploss of the Electric System and Power Output Considering Temperature Effect Input

$ P = P_{arr-t} – (P_{arr-t} * \% P_{Loss}) \ \text{(Equation 36)} $

Where:

$ P = \text{Total output power of the solar array} $
$ P_{arr-t} = \text{Power output considering temperature effect} $
$ \% P_{Loss} = \text{Percentage of power loss} $
$ P = 735,006W – (735,006W * 0.195) = 591,679.83W $

Therefore, the power loss calculation of the solar array yielded a resultant of 591,679.83W. The following phase in the calculation of solar array energy production is to ascertain the daily power output that the PV modules will generate, utilizing the resultant total power as described in equation 36. The average number of peak sun hours in Puerto Rico is 5.5 per day. The solar array will generate the following power in a day, as indicated by equation 37:

$ E_{daily} = 591,679.83W * \frac{1kW}{1000W} * \frac{5.5hr}{1day} = 3,254.24 \frac{kWh}{day} \ \text{(Equation 37)} $

Equations 38 and 39 can be employed to determine the total AC power generation of the solar array over the course of the month and the year.

$ E_{monthly} = E_{daily} * \frac{30 days}{1month} = 97,627.17 \frac{kWh}{month} \ \text{(Equation 38)} $
$ E_{yearly} = E_{monthly} * \frac{12months}{1year} = 1,171,526.1 \frac{kWh}{year} \ \text{(Equation 39)} $

Consequently, the solar array’s annual AC energy production is estimated to be 1,171,526.1kWh

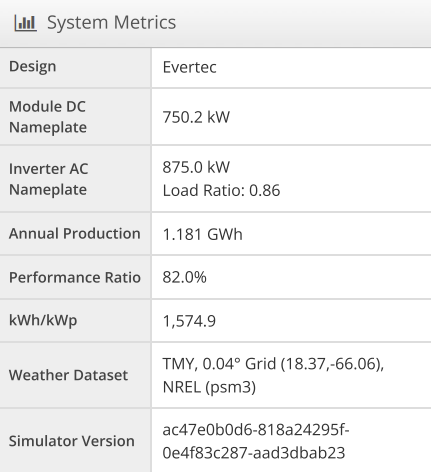
Figure 26: Evertec’s System Metrics

Analysis of results for Evertec

Upon acquiring the theoretical outcomes for the photovoltaic system regarding system size and yearly output rates, these figures may be similar to those produced by the Helioscope software. The engineering report in Helioscope provides accurate numbers derived from the provided data. Analysis of the findings reveals a minimal percentage error, as seen in Equation 40 and Table 29.

$ \text{Percentage Error %} = \frac{| \text{Simulation} – \text{Theoretical}|}{\text{Theoretical}} * 100 \ \text{(Equation 40)} $

Evertec	Theorical Values	Helioscope Values	%Error
System Sizing	750,000 W	750,200 W	0.026%
Yearly Energy Production	1,171,526.1 KWh	1,181,496.6 KWh	0.85%

Table 29: Summary of the Comparison of the Theoretical results and Helioscope Results

The Homer simulations provide a comprehensive evaluation of monthly energy generation, energy use, operational expenses, and specific energy output for each contributing system. These systems consist of Luma Energy, cogeneration, and a photovoltaic system. First is to analyze Evertec’s electricity use with Luma as the only supplier. Subsequently, model the utility in Evertec alongside CHP. A micro-grid system will be developed to integrate all diverse energy sources. The figures below illustrate the energy distribution from several sources to Evertec, the energy output of these sources, and the potential cost implications associated with each energy source. Three scenarios were analyzed: using just the local utility, employing both the local utility and CHP as energy sources, and finally, integrating CHP, local utility, and a PV system (as per Helioscope findings). The Homer simulation requires the inclusion of a boiler in the system, although under ideal specs, since Evertec lacks a boiler in its electrical system. This component exists only for simulation reasons and will not influence the simulation’s result. The electric load and thermal load in the system will remain constant throughout the runs. The conclusive simulation included all systems, linking the photovoltaic specs and system inputs to the Homer simulations from Helioscope. This is the essential element to note.

Initially, in the simulation of Evertec’s electric system prior to the construction of the CHP units, Evertec only relies on electricity from the utility. Utilizing the electric consumption data from 2019, together with the price per kilowatt-hour and the sellback rate for the energy produced by Evertec that is not used internally. Evertec does not generate its own energy; hence, the sellback price is irrelevant. All required data for executing this simulation is detailed in table 30 and the data is located in their separate tabs as seen in figures 26 and 27.

Energy Consumed in 2019 (KWh)	Daily Energy Consumed in 2019 (KWh)	Average Grid Power Price in 2019 ($/KWh)
11,515,898	31,550.4	0.205

Table 30: Input Data for Utility Only Homer Simulation

Figure 26: Homer Electric Load Input.

Figure 27: Homer Grid Power Price Input for 2019

Furthermore, figure 28 presents a monoline design illustrating the system’s functionality and the interconnection of all components in 2019.

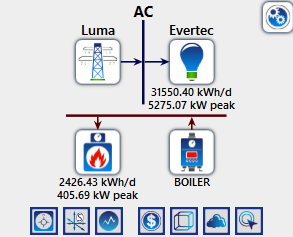
Figure 28: Homer LUMA Breakdown of Energy Transmission.

Upon running all parameters required for the first simulation, figure 29 presents an electric load profile for Evertec’s consumption in 2019, while figure 30 provides a comprehensive cost summary outlining the operational and maintenance expenses of the systems.

A screenshot of a graph

Description automatically generated Figure 29: Homer Simulation Results only LUMA (Before Cogeneration Plant).

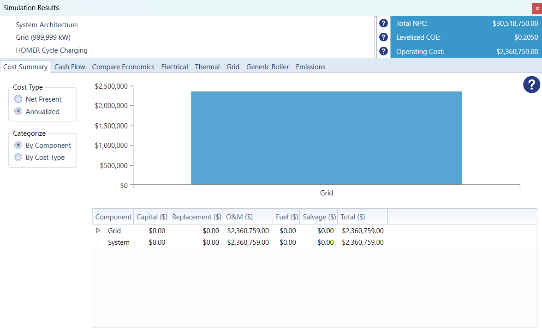
Figure 30: LUMA Only Costs Results.

Upon simulating the system for the year 2019, the findings align closely with the actual outcomes for Evertec throughout that year. Homer delivers precise and comprehensive figures drawn from the data provided. However, it’s important to note that Homer does not account for fluctuations in grid power prices, maintenance, and shutdowns of the CHP system resulting from various component failures and mismatches. This component influences the error rate between the real numbers and the simulation results. The analysis indicates a minimal error percentage, as seen in equation 41 and table 31.

$ \text{Percentage Error %} = \frac{| \text{Simulation} – \text{Real} |}{\text{Real}} * 100 \ \text{(Equation 41)} $

Evertec	Real Values	Homer Values	%Error
Yearly Energy Consumption	11,515,898 KWh	11,515,896 KWh	0.000017%
Grid Cost	$2,235,390.47	$2,360,759	5.60%

Table 31: Summary of the Comparison of the Theoretical results and Homer Results in 2019

Following the simulation of the system with just the utility, the subsequent simulation occurs post-installation of the CHP system. This system offers a comprehensive overview of Evertec’s energy use. Evertec’s energy production and the sellback price, together with energy demand, are shown in Table 32.

Energy Consumed in 2019 (KWh)	Daily Energy Consumed in 2019 (KWh)	Average Grid Power Price in 2022 ($/KWh)
11,515,898	31,550.4	0.35

Table 32: Input Data for Utility and CHP System Homer Simulation

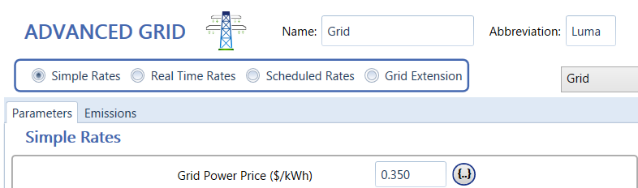
Figure 31: Homer Grid Power Price Input for 2022

Clearly, figure 32 delineates all necessary parameters for Homer to replicate the CHP system. In the Generator tab, the capital represents the total cost per kilowatt of the CHP system, totaling $11,000,000. All parameters are specified in table 33. Furthermore, in figure 32, one of the factors required by the Homer simulation software is the fuel price for natural gas in $/m3.

To obtain this data, the $11/mmbtu must be converted to the specified units of $/m³, as previously indicated. This conversion is performed in equation 42 below. Finalizing this conversion requires using the estimate of 1 mmbtu = 26.81 m³.

$ \frac{\$}{m^3} = \frac{\frac{\$ 11}{1mmBTU}}{\frac{1mmBTU}{26.91m^3}} = \$ 0.41/m^3 \ \text{(Equation 42)} $

The value obtained from equation 42 is going to be used in the natural gas fuel price option on figure 32.

Parameters	Values
Capital ($)	4,538.34
O&M ($/op.hr)	0.018
Minimum Load Ratio (%)	55
CHP Heat Recovery Ratio (%)	80
Natural Gas Fuel Price ($/m^3)	0.41

Table 33: CHP Model Parameters for Homer Simulation

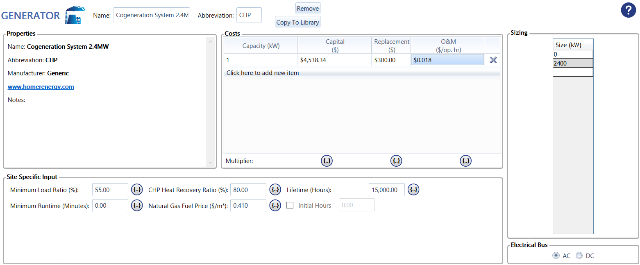
Figure 32: Homer CHP Specification Input

Similarly, figure 33 presents a monoline design illustrating the system’s functionality and the interconnection of all components in 2022 when the CHP system was installed.

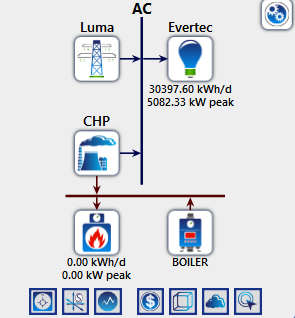
Figure 33: Homer LUMA and CHP Breakdown of Energy Transmission.

Subsequently, executing all parameters necessary for the first simulation, figure 34 illustrates an electric load profile for Evertec’s consumption in 2022, while figure 35 offers a detailed cost breakdown delineating the operating and maintenance expenditures of the systems.

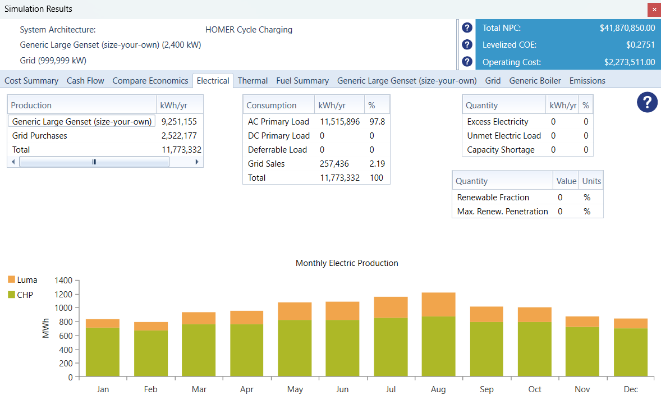
Figure 34: Homer Simulation Results LUMA and CHP (After Cogeneration Plant).

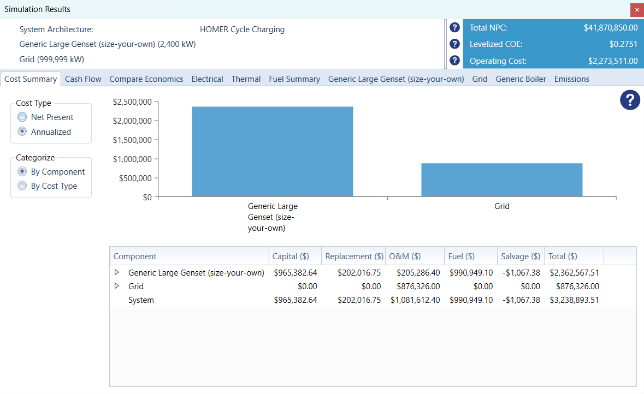
Figure 35: LUMA and CHP Costs Results.

The simulation of the system for 2022 yielded results that closely correspond with Evertec’s real performance during that year. Homer presents accurate and thorough statistics derived from the supplied data. Nonetheless, it is crucial to acknowledge that Homer does not include variations in grid power costs, maintenance, and the shutdowns of the CHP system due to diverse component failures and discrepancies. This component affects the discrepancy rate between the actual values and the simulated outcomes. The study reveals a negligible error percentage, as seen in equation 43 and table 34.

$ \text{Percentage Error %} = \frac{| \text{Simulation} – \text{Real} |}{ \text{Real} } * 100 \ \text{(Equation 43)} $

Evertec	Real Values	Homer Values	%Error
Yearly Energy Consumption (Grid)	2,789,160 KWh	2,522,177 KWh	9.57%
Grid Cost	$925,275.77	$876,326	5.29%
Yearly Energy Production (CHP)	8,877,820 KWh	9,251,155 KWh	4.20%

Table 34: Summary of the Comparison of the Theoretical results and Homer Results in 2022

Completing the simulation of the system including the utility, the CHP system, and a newly designed PV system. This system provides a thorough analysis of Evertec’s energy use. The energy output of Evertec, the sellback price, the yearly energy production of the PV system, and the energy consumption are shown in Table 35.

Energy Consumed in 2019 (KWh)	Daily Energy Consumed in 2019 (KWh)	Average Grid Power Price in 2024 ($/KWh)	Grid Sellback price ($/KWh)
11,515,898	31,550.4	0.38	0.025

Table 35: Input Data for Utility, CHP System and PV System Homer Simulation

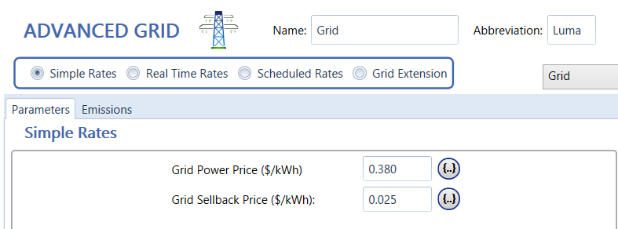
Figure 36: Homer Grid Power Price Input for 2024

Furthermore, figure 37 outlines the essential characteristics for Homer to duplicate the CHP system. All parameters are delineated in table 36. Additionally, in figure 37, a necessary component for the Homer simulation program is the fuel price for natural gas expressed in $/m3. For this data to be obtained, a conversion has to be made from $11/mmbtu to the designated units of $/m3. The contracted price with the LNG provider is $11 per mmbtu. This conversion is performed, and the price is 0.41 ($/m3) as listed below.

Parameters	Values
Capital ($)	4,538.34
O&M ($/op.hr)	0.018
Minimum Load Ratio (%)	55
CHP Heat Recovery Ratio (%)	80
Natural Gas Fuel Price ($/m^3)	0.41

Table 36: CHP Model Parameters for Homer Simulation

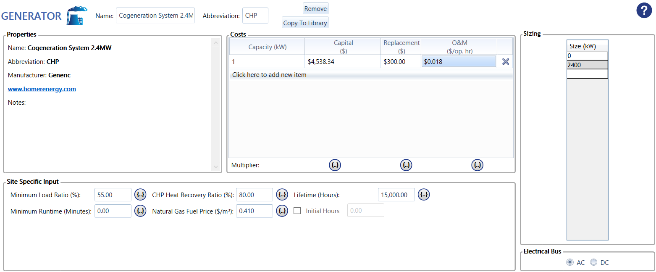
Figure 37: Homer CHP Specification Input

Likewise, figure 38 depicts a monoline architecture that illustrates the system’s operation and the connectivity of all components in 2024.

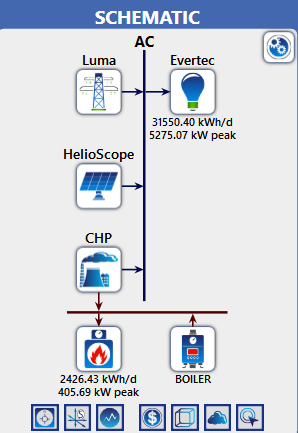
Figure 38: Homer LUMA, PV System and CHP Breakdown of Energy Transmission.

Following the execution of all necessary parameters for the first simulation, figure 39 presents an electric load profile for Evertec’s consumption forecast in 2024, while figure 40 provides a comprehensive cost analysis outlining the operational and maintenance expenses of the systems.

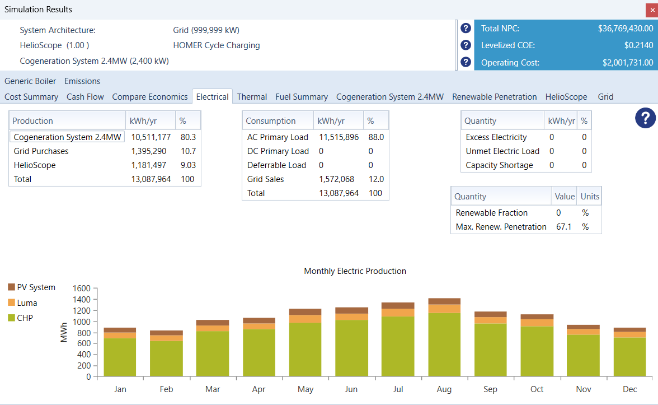
Figure 39: Homer Simulation Results LUMA, PV System and CHP (After Cogeneration Plant with PV System).

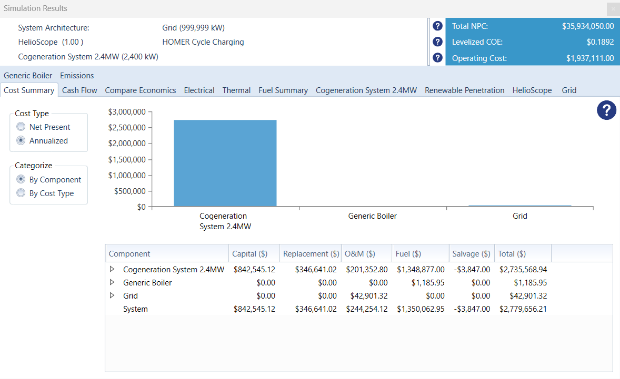
Figure 40: LUMA, PV System and CHP Costs Results.

The system simulation for the 2024 prediction yields findings that closely align with Evertec’s actual projections. Homer provides precise and comprehensive statistics based on the given data. Projection for 2024 is detailed in table 37. It is essential to recognize that Homer omits changes in grid power prices, maintenance, and the shutdowns of the CHP system resulting from various component failures and inconsistencies. This component influences the variance between the real values and the simulated results. The research indicates a minimal error percentage, as seen in equation 44 and table 38. Correspondingly, equation 45 is used to determine the annual KWh consumption of Evertec due to peak load and other discrepancies.

Projection 2024
AEE y AAA 2019-2020 Cost	2,422,804.23
Operation Cost CHP 2024	157680
Maintenance Cost CHP 2024	182,912.40
Water Billing Cost 2024	214,641.04
Utility Cost 2024	412,976.51
Maintenance Cost Chillers 2024	20,000
LNG Cost 2024	993284.47
Total Cost 2024	1981494.42
Annual Savings 2024	441,309.81

Table 37: 2024 Yearly Cost and Savings Projections

$ \text{Percentage Error %} = \frac{|Simulation-Real|}{Real} * 100 \ \text{(Equation 44)} $
$ \text{Grid Estimate Cost} = \frac{\text{Total Annual Grid Cost}}{\text{Average Grid Power Price in 2024}} * 100 \ \text{(Equation 45)} $

Evertec	Homer Projection
Yearly Energy Consumption (Grid)	112, 897 KWh
Grid Estimate Cost per Year	$42,901.32
Yearly Energy Production (CHP)	10,511,177 KWh

Table 38: Summary of Homer Projections for 2024

Economic Analysis

Starting with the cost analysis of the cogeneration system, table 39 provides a comprehensive summary of all the components necessary to operate the system and generate the energy necessary for the operations of Evertec’s facilities. To begin with the economic analysis of the CHP system, it is necessary to examine the initial investment of the undertaking.

Elements	Price ($)
Equipment	5,315,602.01
Two Co-Generators of 1.2MW each	1,735,084.96
Two Absorption Chillers of 350 tons each	1,148,000
Energy Storage System 1.5MW, with 750kW in batteries	1,019,279.00
Step-Up Transformer; 480V to 13.2kV	151,974.50
Incoming/Outgoing Switch setup	172,825.00
Three Cooling Towers, 600 tons each and a sweeper (filter)	763,316.00
Various pumps for chilled water, condensed water, and heat exchanger	146,276.55
Motor Control Center (MCC)	178,846.00
Building for the Combined Heat and Power (CHP) unit	2,535,148.04
Structural Station for LNG	676,076.39
Electrical and Control Systems	675,528.83
Mechanical and Control Installation materials	3,078,291.06
Total Initial Investment	11,000,000

Table 39: Project Initial Investment

Evertec of Cupey made a strategic initial investment of approximately 11 million dollars in a cogeneration plant system in 2021, which consists of 2 cogeneration plants of 1.2MW each. The approach towards the data provided by the corporation is to navigate through the company’s energy expenditure before and after this significant investment to obtain a simple payback period which will tell the viability of this project.

The previous comprehensible data about the initial investment made by the company for the cogeneration plants was made strategically to ensure effectiveness and efficiency in its implementation, which cost them as mentioned before 11 million dollars and reduced more than 50% from the energy consumption from the utility as it is described in table 22 vs table 23. The investment reflects the corporation’s commitment to economic savings and environmental stewardship. This cogeneration system was designed to address the bank’s unique energy requirements while maintaining ambitious standards of environmental sustainability, reducing costs and consumption from the utility and reaching a certain quantity of savings under a period in which they can accomplish their objective of recovering the initial investment in the best time possible.

The objective to be completed is to compare the data recorded before and after the Cogeneration System was implemented in the facilities of Evertec. The base time before cogeneration installation is the year 2019, followed by 2020; to start calculating the electric utility energy consumption in kWh by Evertec buildings and their expenses for the same.

Table 22 shows the total electric utility energy consumption in kWh and the total cost of the energy consumed in 2019 and in 2020, which means before the Cogeneration System was implemented. Evertec consumed 11,095,128.00 in 2019 and 10,553,400.00 in 2020, the first one being the peak; paying a total of $2,235,390.4 and $1,981,063.7, respectively. These values are particularly important to compare this data with the consumed energy after the cogeneration was installed because it tells in proportion to the total consumption, how much less is now required from the grid. In addition to this, how much fuel is being paid for the cogenerators. Therefore, by obtaining how much money the company is saving monthly and yearly, it gives the opportunity to calculate a simple payback period.

Total Energy (kWh)	Total Cost ($)
11,095,128.00	2,235,390.4
10,553,400.00	1,981,063.7

Table 40: Energy Consumption and Costs BEFORE cogeneration.

Now, the same will happen after the cogeneration plant is installed in the year 2021. The data for subsequent years is going to help with the comparison of energy consumption and its cost before and after the Cogeneration System installation. This approach provides a clearer view of the annual average savings Evertec receives and the reduced reliance on electrical utility. In table 23 and 24, the total electric utility energy consumption in kWh with its monthly average and the total cost of the energy consumed with its monthly average, for years 2021 to 2024.

Achieving better precision at the results, in 2024, which has not ended yet, the total cost was divided between 9 months which are the total months of given data, to obtain an average monthly cost and the same for the average energy consumed. In this data it is noticeable that the reduction from using the electric utility was more than 50% in comparison to table 14.1 and over a million dollars of savings; even almost two million dollars of saving as shown in 2023, $407,919.12 and $309,732.38. While in 2019 it was $2,235,390.4 and in 2020 $1,981,063.7. From the electric utility there is a huge amount of savings from energy consumption and the cost of it. It will be seen down in the last tables of this section (table 41). It must be indicated that these savings apply to the fuel cost by year.

Total Cost ($)

2,235,390.4

1,981,063.7

407,919.12

309,732.38

Table 41: Electric Utility Energy Consumption and Costs AFTER cogeneration, data by Evertec.

Another crucial piece of data for the analysis is shown in table 42, which is the energy production and costs of LNG fuel by year. This table will show the total energy produced in mmBtu with its monthly average energy production and the total cost for that energy produced with its monthly average cost, for years 2021 to 2024. This value of monthly average cost and energy was computed manually using as reference the 4 excel data sheets which are indicated in the table below; just by dividing the total of both categories each year by 12, which is the total months in a year. The total cost was divided by 9 months, which are the total months of given data, to obtain an average monthly cost and the same was done for the average energy consumed.

Year	Total Energy (mmBtu)	Average Energy (mmBtu)	Total Cost ($)	Average Cost ($)
2021	66,920.01	5,576.67	736,150.14	61,345.85
2022	80,666.30	6,722.19	885,983.51	73,831.96
2023	93,953.38	7,829.45	1,026,094.23	85,507.85
2024	68,035.76	7,559.53	744,963.35	82,773.71

Table 42: Energy Production and Costs of LNG fuel, data by Evertec.

A total of $797,229.16 in the entire year, and to see the average cost paid to LUMA per month, it was divided by 12, giving $66,435.76/month. The total that was paid in that year was more than 1 million dollars less than what was being paid to the utility services before the cogeneration. These cost breakdowns can be observed below, in table 43.

Total Cost ($)

797,229.16

66,435.76 per month

Table 43: Values obtained from billing tables in Chapter 14.

Upon the establishment of the cogeneration facility that was recently installed in 2021, the cost that the client, Evertec was paying for electricity services to the utility. A total of $797,229.16 in the entire year, and to see the average cost paid to LUMA per month, giving $66,435.76. The total paid in 2021 was more than 1 million dollars less than before the cogeneration.

Metric (Avg)	Annually	Monthly
Before Cogen (kWh)	10,824,264	902,022
Before Cogen ($)	2,108,227.13	175,685.59
After Cogen (kWh)	2,208,354.67	184,029.56
After Cogen ($)	650,708.38	54,225.7

Table 44: Annual and monthly average Energy Consumption from utility and its costs, Before and After Cogeneration System installation.

Another observation from table above is that the energy consumption after the Cogeneration System was implemented, from the electric utility, was 80% less than before the installation. This reduction in consumption of energy from the grid reduces the cost, which was about 1.6 million dollars approximately. Furthermore, this does not consider the LNG fuel and water consumption cost.

A summary of the values as averages is seen in table 45; is going to present fuel consumption in mmBtu by CHP plants, and their cost. This is calculated using the given data by Evertec of the years 2021 to 2024. Since 2024 is not finished, a projection was necessary to calculate the monthly averages of the pertinent values to then obtain the annual average). The average monthly rate indicated below in table 16.7 uses the months of all the 4 years (with the adjustment of 2024 which is incomplete) and its costs.

Description	Average Monthly	Average Annually
Energy (mmBtu)	6,682.3032	80,187.64
Cost ($)	73,247.06	878,964.75

Table 45: Annual and monthly averages of fuel Consumed by the CHP plant and its cost.

The savings calculations conducted after the cogeneration plant implementation, which utilizes natural gas as its primary fuel, necessitate an assessment of Evertec’s expenditures on water services prior to and following the installation of the cogeneration system. Incorporating these figures into the final calculations is essential for the reliability of the simple payback period.

As shown in Table 44 illustrates the yearly average payment made to the utility. Prior to the establishment of the CHP system, the customer paid $2,108,227.13 to LUMA. Following the cogeneration plant, Evertec paid $650,708.38 monthly. The subtraction from these two quantities yields an average yearly saving of $1,457,518.75. However, this figure does not represent a genuine saving, as it must be adjusted by deducting the annual average expenditures associated with LNG fuel and other charges that will be elaborated upon later. This figure pertains only to the electric utility savings and does not reflect the company’s savings after the implementation of the cogeneration system as illustrated in table 46 below.

Avg Annual Saving ($)

1,457,518.75

Table 46: Average Annual Savings calculated

Using table 25 which includes the water billings before and after cogeneration system, this is an additional cost that must be included for the savings and simple payback period, due to the rise in water usage from the chillers implemented with the CHP system. The annual average water billing cost difference between before and after cogeneration system is the value to consider for this additional water cost, which will be included in table 47.

The data shows no substantial difference in terms of the water volume used. Before the cogeneration, the annual average was 26,623m³and after, 32,864.8m³. However, there was a significant difference in price, prior to the cogeneration installation, the annual average of 2019 to 2020 was $180,805.21 and the average for 2021 to 2024 was $236,590.28, meaning that the cogenerators water consumption difference in cost on average is $55,785.08 to the bill annually.

Avg. Water Volume Before	26,623m³
Avg. Water Volume After	32,864.8m³
Avg. Yearly Cost Before	180,805.21
Avg. Yearly Cost After	236,590.28,
Avg. Difference Cost Before vs After	55,785.08

Table 47: Annual average water consumption and its cost Before and After Cogeneration System installation.

Concluding the planning costs and obtaining the annual savings for the payback period, the expenses for maintenance and operations of the cogeneration system are to be considered acquiring a correct payback period.

The CHP plant has 4 operators with a total salary of $157,680 paid annually. Given maintenance, there is a variation in costs due to the need for the cogeneration plant in each particular year. These costs, regardless of annual variability, have a contract which established a number indicating the monthly cost that it would be paid for the entire year (which does not change). Evertec supplied data for CHP’s maintenance, which is illustrated in table 48 to 51, and $20,000 in chiller maintenance.

Annual Savings 2021
AEE y AAA 2019-2020 Cost	2,422,804.23
Operation Cost CHP 2021	157680
Maintenance Cost CHP 2021	148,945.80
Water Billing Cost 2021	240,326.73
Utility Cost 2021	797,229.16
Maintenance Cost Chillers 2021	20,000
LNG Cost 2021	736,150.14
Total Cost 2021	2,100,331.83
Annual Savings 2021	322,472.40

Table 48: Annual Savings 2021

Annual Savings 2022
AEE y AAA 2019-2020 Cost	2,422,804.23
Operation Cost CHP 2022	157680
Maintenance Cost CHP 2022	148,945.80
Water Billing Cost 2022	245,646.73
Utility Cost 2022	925,275.77
Maintenance Cost Chillers 2022	20,000
LNG Cost 2022	885,983.51
Total Cost 2022	2383531.81
Annual Savings 2021	39,272.42

Table 49: Annual Savings 2022

Annual Savings 2023
AEE y AAA 2019-2020 Cost	2,422,804.23
Operation Cost CHP 2023	157680
Maintenance Cost CHP 2023	182,912.40
Water Billing Cost 2023	260,506.74
Utility Cost 2023	407,919.12
Maintenance Cost Chillers 2023	20,000
LNG Cost 2023	1,026,094.23
Total Cost 2023	2055112.49
Annual Savings 2023	367,691.74

Table 50: Annual Savings 2023

Annual Savings 2024
AEE y AAA 2019-2020 Cost	2,422,804.23
Operation Cost CHP 2024	157680
Maintenance Cost CHP 2024	182,912.40
Water Billing Cost 2024	214,641.04
Utility Cost 2024	412,976.51
Maintenance Cost Chillers 2024	20,000
LNG Cost 2024	993284.47
Total Cost 2024	1981494.42
Annual Savings 2024	441,309.81

Table 51: Annual Savings 2024

The first step towards the simple payback period for the cogeneration plant includes LNG fuel and all additional costs. This shows how long the investment will be repaid in terms of years. Firstly, the project’s first investment payment and the annual savings from 2021 to 2024 are required to perform equation 46. Additionally, the annual savings were calculated by using the total cost that the client paid before and after the cogeneration plant installation, including electricity, water, and other services. This simple payback period calculation is demonstrated below.

$ \text{Simple Payback Period (years)} = \frac{\text{Project Initial Cost}}{\text{Annual Savings (2021 to 2024)}} \text{(Equation 46)} $
$ \text{Simple Payback Period (years)} = \frac{11,000,000}{1,170,746.37} = 9.39 \text{Years} $

The cogeneration plant has the option to use propane gas as fuel, but it does not last long since it operates at 70% efficiency, meaning that you can only refill propane gas up to 33,600 gallons. Unlike LNG fuel, which operates at 90% efficiency, and it can fill storage tanks up to 43,200 gallons. Propane gas is more volatile, and because of this, it loses more energy on heat and can’t be filled up all the way. Additionally, propane gas lasts way less than LNG, with 10,000 gallons of propane, the cogeneration plant only lasts 24 hours a day for 4 days, while with LNG fuel it lasts 24 hours a day for 20 days. If it is assumed that both fuel sources are used simultaneously, with 40,000 gallons each, propane gas would last approximately 12 days, whereas LNG would last the same amount of time as mentioned before. Even though propane is less ideal, the cogeneration plant can still use it, and it can be considered for emergency situations, and in this section, the prices per units of LNG and propane will be compared by converting propane gas units of $/gallons to $/mmbtu (since LNG is already in units of $/mmbtu). Gas companies were contacted to find prices of propane, and the average of all the prices found is $4/gallon, whereas the LNG is at $11/mmbtu because Evertec has a contract with New Fortress Energy which buys the fuel at the price mentioned. After researching on the internet, 1 gallon of propane is approximately 0.091500 mmbtu, and with this, the conversion of propane units can be started. This process is shown below on equation 47.

$ \frac{\$ 4}{gallon} * \frac{1gallon}{0.091500mmBTU} = \$ 43.715/mmBTU \ \text{(Equation 47)} $

LNG ($/mmbtu)	Propane ($/mmbtu)
11	43.715

Table 52: Comparison of propane and LNG fuel sources.

As observed above, in table 52, propane gas is valued approximately at $43.715/mmbtu, and LNG is valued at $11/mmbtu. With this comparison, LNG is way more cost efficient than propane, and as explained before, it is more energy efficient too. Besides, it is not possible to compare with the historical records the usage of propane gas in the cogeneration plant at Evertec since it has only been used twice because of how expensive and inefficient it is.

The initial expenditure for the Photovoltaic System will be detailed in the subsequent section, including construction, solar panels, and further components to consider. Regarding the projected value of each component for the initial investment, the total final cost to execute this system as an integration into the Evertec Cupey micro-grid includes extra expenses such as solar panel maintenance and any other applicable charges. Furthermore, a projected evaluation of the savings generated by Evertec Cupey via the integration of the PV system into their micro-grid, juxtaposed with the savings realized after the establishment of the cogeneration plant in 2022. In 2023, the integration of the cogeneration plant resulted in total savings of $526,632.84; however, this figure is subject to variability due to the unpredictability of future utility costs. Consequently, this amount will serve as the foundational basis for economic analysis. This comparison will determine the viability of implementing the PV system into their micro-grid, necessitating a final estimate of the payback period required to repay the investment.

The entire payout for the electric bill in 2024 amounts to $412,976.50, as provided by Evertec Cupey. This base value will facilitate the comparison with the savings generated by the implementation of the PV system and its investment payback term to assess its viability. Determining the energy price established by LUMA, a foundational price of $/kWh is required for the planning costs of the PV system and the anticipated savings for Evertec, including the predicted payback time; Equation 48 will facilitate this analysis.

$ \text{LUMA}(kWh) = \frac{\text{Monthly Bill Price}}{\text{Monthly Consumption (kWh)}} \ \text{(Equation 48)} $

Table 53 will be utilized in conjunction with Equation 47, which delineates the billing for the last seven months of 2024; thus, an estimated price per kWh for the year 2024 can be derived, establishing a standard basis for the analysis of subsequent years and calculating the annual savings alongside the payback period of the photovoltaic system investment. Accompanying the 2024 power bill figures used for the computation, $412,976.50 paid by Evertec to LUMA in the previous year (2024) will be included. The savings presented at the conclusion of this chapter will be more precise and authentic; this is due to the significant fluctuations in electric bill costs over short intervals, rendering it impossible to ascertain an exact figure for the actual savings. However, by utilizing the 2024 bills up to September, the most recent one, it is feasible to derive a highly accurate annual savings estimate.

2024 Monthly Utility Bills	Energy Consumed (kWh)	Cost ($)
January	64,680	25,940.54
February	47,520	23,269.11
March	124,800	39,570.79
April	52,800	23,896.92
May	97,020	33,938.53
June	163,020	49,391.05
July	70,356	31,159.58
August	142,824	46,680.96
September	93,060	35,884.90
October	–	–
November	–	–
December	–	–

Table 53: 2024 Electric utility bills costs AFTER Cogeneration, data from Evertec Cupey

A comparison will be conducted using the entire amount Evertec paid LUMA in 2024, factoring in the cogenerators operation. This analysis will simulate yearly usage as if the photovoltaic system were in place, given that the cogeneration plant supplies 2.4MW and the photovoltaic system produces 600kW after DC to AC conversion.

Additionally, Table 54 provides a comprehensive summary of all expenditures associated with the PV system, including design expenses, electrical components, mechanical and civil materials, wiring, feeders, and installation. The total cost for the PV system is listed below.

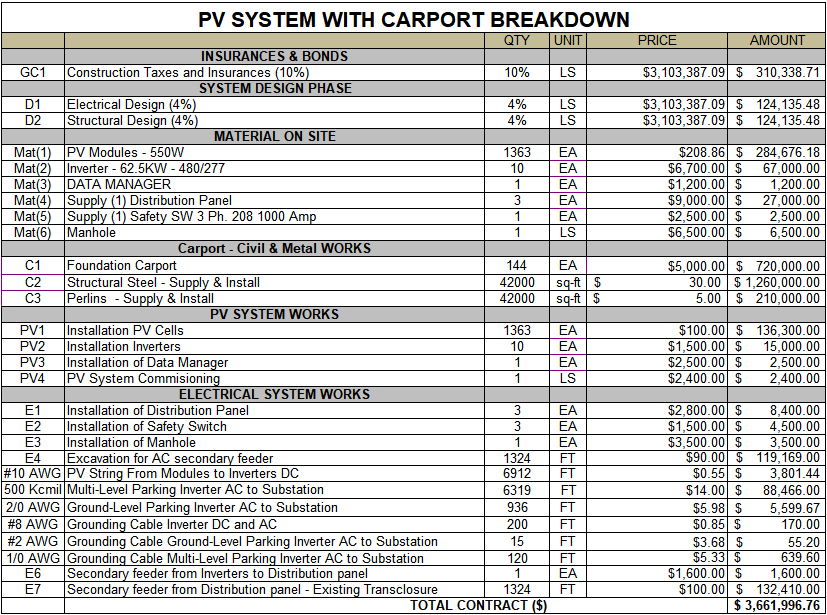
Table 54: PV System with Carport Breakdown

The PV system economic analysis focuses on the year 2024 which is the year where it is going to be implemented since it does not exist physically yet in Evertec. Moreover, the year has not ended, this is why taking an average cost of the current utility price, and the calculation yielded $0.3852/kWh. Furthermore, the PV system generates 1,181,496.6 kWh annually, and a rough estimate can be made on how much the customer would pay the utility, and this is the savings used for the calculations below. This is done by multiplying the kWh generated by the PV system with the average cost of energy provided by LUMA. This is done below on equation 49, where it is obtained how much Evertec is supposed to pay for energy to the utility grid. Additionally, to calculate the savings that the PV system will produce, a difference must be made between the current price of electricity that the client pays and the price if the PV system was installed. This calculation is done below, in equation 50. Finally, table 55 indicates a breakdown of how much Evertec pays with and without the PV system. It also shows the approximate payback period which uses equation 41, and this calculation is shown below.

$ \text{Cost} = 0.3852 \frac{\$}{kWh} * 1,181,496.6kWh = \$ 455,112 \ \text{(Equation 49)} $
$ \text{Savings} = |\text{(Cost Without PV)} – \text{(Cost With PV)}| \ \text{(Equation 50)} $
$ \text{Savings} = | \$ 412,976.50 – $\ 445,112 | = \$ 42,135.50 $

Description	Amount
Initial Investment	$3,661,996.76
Annual Operational and Maintenance Costs	$0.00
Energy produced by PV System (kWh annually)	1,181,496.6 1,181,496.6
Annual Energy Cost without PV System (2024)	$412,976.50
Annual Cost of Energy (Average 2024)	$0.3852/kWh
Annual Energy Savings with PV System (2024)	$455,112
Energy Costs Savings (2024)	$42,135.5
Payback Period (Years)	8.04 years

Table 55: PV System costs breakdown with simple payback period.

Table 55 indicates a breakdown of how much our Evertec pays with and without the PV system. It also shows the approximate payback period. The PV system has the potential to produce more energy than demanded by Evertec from the utility. Therefore, at the same rate, this system would cover the annual electric bill for Evertec and produce an additional $42,235.5. This indicates that Evertec can consume more electricity and still pay zero dollars to LUMA.

The annual energy savings from the PV system, amounting to $455,112, represents the overall savings generated by Evertec. Additionally, supposing the customer would proceed with the investment, calculations were conducted for a loan of 3,661,996.76 at an interest rate of 7% and a duration of 12.3 years. Finally, equations 16.7 and 16.8 show the calculations for the true annual payment made towards the loan.

Finalizing the economic analysis, table 16.18 has the comparison between the PV and CHP systems. It summarizes all the calculations done up to this point, and the data given to us by the client. The table has the initial investment, annual cost for electricity, and annual cost for operational and maintenance. Additionally, all these comparisons happen in the current year, 2024.

$ A = P * \frac{i(1+i)^n}{(1+i)^n – 1} \ \text{(Equation 16.7)} $

Where:

$ A = \text{Annual Payment} $
$ P = \text{Initial Investment} $
$ i = \text{Interest Percentage} $
$ n = \text{Total Years} $

$ A = 3,661,996.76 * \frac{0.07(1+0.07)^{12.3}}{(1+0.07)^{12.3} – 1} \ $
$ A = 3,661,996.76 * 0.12395 = \$ 453,759.86 \ $

Now, we will calculate the total interest paid over a span of 12.3 years, utilizing equation 16.8 below. The number displayed will let us know how much the client is going to pay in interest on the loan.

$ I = (A * n) – P \text{(Equation 16.8)} $

Where:

$ I = \text{Total Interest to Pay} $
$ A = \text{Annual Payment} $
$ n = \text{Total Years} $
$ P = \text{Initial Investment} $

$ I = (\$ 453,759.86 * 12.3 \text{Years}) – \$ 3,661,996.76 = \$ 1,915,739.48 $

Ultimately, after consolidating all outcomes from prior calculations, the system’s output is very feasible. After 12.3 years, Evertec will realize the
whole yearly energy savings from the PV system, so contributing to the payback time of the CHP system and greatly reducing costs annually.

Description	Amount
Initial Investment	$3,628,100.02
Annual PV System Operational and Maintenance Costs	$0.00
Annual Energy Cost without PV System (2024)	$412,976.50
Annual Energy Cost with PV System	$0.00
Payback Period PV System (Years)	12.3 years
CHP Project First Investment Payment	11,000,000
Annual Savings (2021-2024)	$404,500.77
Payback Period CHP System (Years)	27.19 years

Table 56: Payback Period Comparison

Conclusion

The design and implementation of a microgrid system incorporating Photovoltaic (PV) technology and cogeneration offers a sustainable and cost-effective solution to address the energy challenges in areas with unstable grids and high electricity costs. By leveraging Puerto Rico’s abundant sunlight, the PV system design provides a renewable source of energy, while the cogeneration system offers backup power and increased efficiency to the system.

The economic analysis compares the initial investment, payback period, and long-term benefits of the cogeneration system and the photovoltaic (PV) system. The following table summarizes the key metrics:

Parameter	Cogeneration System	PV System
Initial Investment	$11 million	$3.6 million
Annual Savings	$404,500.77	$412,966.50
Payback Period	27.19 yrs.	12.3 yrs.
Simulation Error	N/A	0.85%

Table 57: Comparison of PV and Cogeneration Systems.

The cogeneration system requires significantly larger initial investment compared to the PV system. However, this higher upfront expense is offset by the system’s ability to generate substantial annual savings, dramatically reducing utility costs over time. Furthermore, the longer payback period of the cogeneration system reflects the scale of its initial cost, yet its substantial annual savings make it a financially viable solution for achieving sustained reductions in operating expenses.

In contrast, the PV system demands a smaller initial investment and provides a much faster payback period, enabling quicker returns on investment. While it may lead to a slight increase in energy costs during its first year due to installation and operational expenses, it offers meaningful annual savings as energy prices continue to rise, making it an effective option for long-term financial planning. Additionally, simulations for the PV system validated its design with an exceptionally low error margin of just 0.85% when compared to manual calculations, underscoring its reliability. Taking together these systems offer complementary benefits: the cogeneration system excels in delivering significant long-term savings, while the PV system provides faster returns and adaptability to future energy demands. Both systems represent robust strategies for enhancing energy efficiency and reducing costs over time for Evertec.

The integration of these systems not only reduces dependence on the local utility but enhances energy resilience and sustainability by reducing greenhouse gas emissions and energy costs over time. The careful consideration of economic factors, fuel alternatives, and system performance ensures that this solution is financially viable, environmentally responsible, and aligned with local and national energy regulations. Ultimately, this project contributes to advancing energy independence and offers a scalable model for addressing similar energy challenges in other regions.

Bibliography

[1] Sunpower Electronics UK, “What is a Power Converter?” Sunpower UK, Jul. 6, 2015. [Online]. Available: https://www.sunpower-uk.com/glossary/what-is-a-power-converter/.

[2] “Solar Integration: Inverters and Grid Services Basics,” Energy.gov. [Online]. Available: https://www.energy.gov/eere/solar/solar-integration-inverters-and-gridservicesbasics#:~:text=Inverters%20are%20just%20one%20example,input%20becomes%20an%20AC%20output.

[3] “Solar Inverter – What it is and how to choose the right one,” HIES Consumer Code, Jul. 13, 2023. [Online]. Available: https://www.hiesscheme.org.uk/renewable-energy/solar-inverters/.

[4] Anker, “Understanding the Basics: How a DC to AC Converter Works,” Jul. 13, 2023. [Online]. Available: https://www.anker.com/blogs/acpower/understanding-the-basics-how-a-dc-to-ac-converter-works.

[5] “String Inverters vs. Microinverters: Pros and Cons,” 8MSolar, Jun. 9, 2023. [Online]. Available: https://8msolar.com/string-inverters-vsmicroinverters/#:~:text=Pros%20of%20String%20Inverters&text=Easier%20troubleshooting%3A%20One%20of%20the,your%20solar%20system%20running%20again.

[6] “Energy Storage and Power Conversion System (PCS) Test Regulations and Requirements,” All About Circuits. [Online]. Available: https://www.allaboutcircuits.com/industrywebinars/energy-storage-and-power-conversion-systempcstestregulationsandrequirements/#:~:text=A%20Power%20Conversion%20System%20(PCS,and%20off-line%20switching%20functions.

[7] B. P. Sales, “Types of Automatic Transfer Switches & How They Work,” *Buckeye Power Sales*, Jan. 11, 2024. [Online]. Available: https://ps.buckeyepowersales.com/types-automatic-transfer-switcheswork/#:~:text=There%20are%20four%20types%20of,Switch%2C%20and%20Bypass%20Installation%20ATS.

[8] “Overview of 3 types of solar panel array mounts,” Solar Always. [Online]. Available: https://www.solaralways.com/types/array-mount.

[9] “Roof Mounts for Solar Panels,” altEstore.com. [Online]. Available: https://www.altestore.com/store/solar-panel-mounts/roof-mounts-for-solarpanelsc460/#:~:text=Solar%20Panel%20Mounting%20Rails%20are,ground%20up%20into%20the%20structure.

[10] S. Admin, “What is solar rail splice,” Solar Parts and Components Factory Direct, Jun. 24, 2021. [Online]. Available: https://www.solarpartscomponents.com/what-is-solar-railsplice.

[11] H., “Battery Energy Storage System Components and Their Functions,” IGOYE Solar Energy Equipment, Jan. 2, 2024. [Online]. Available: https://igoyeenergy.com/battery-energy-storage-system-components/.

[12] D. Kos, DC – Distribution and Protection. Etigroup. [Online]. Available: https://www.etigroup.eu/solution/protection-of-photovoltaics-systems/dcdistribution-and-protection.

[13] Solar Circuit Protection Ltd., Solar PV System Circuit Protection Guide. [Online]. Available: https://www.swecheck.com.au/editorials/solar-pv-circuit-protectionguide.php#:~:text=Fuse%20Protection%20for%20PV%20Arrays&text=A%20fuse%20link%20on%20each,can%20continue%20to%20generate%20electricity.

[14] Everything You Need to Know About Rapid Shutdown. Tigo Energy. [Online]. Available: https://www.tigoenergy.com/post/blog-everything-you-need-to-know-aboutrapidshutdown#:~:text=Rapid%20shutdown%20provides%20a%20safe,and%20efficiently%20avoiding%20electrical%20hazards.

[15] Direct Current – Energy Education. [Online]. Available: https://energyeducation.ca/encyclopedia/Direct_current.

[16] N. Seghers, “What is a Critical Load Panel? [+Diagram],” Clever Solar Power, Sep. 25, 2023. [Online]. Available: https://cleversolarpower.com/what-is-a-critical-load-panel/.

[17] S., “NEC 2020 Rapid Shutdown Requirements,” Mayfield Renewables, Jun. 6, 2023. [Online]. Available: https://www.mayfield.energy/technical-articles/nec-2020-rapid-shutdownrequirements/.

[18] “Can I Add a Solar Panel to My Existing Array?” Pacific Yacht Systems. [Online]. Available: https://www.pysystems.ca/resources/boating-tech-talk/can-i-add-a-solar-panel-to-my-existing-array/.

[19] How to Wire Solar Panels in Parallel or Series, HK MICNO Electric Co., Ltd. [Online]. Available: https://www.micnoenergy.com/content/?466.html.

[20] National Renewable Energy Laboratory (NREL), Personal Protective Equipment Selection for Solar Panel Installers, Solar Energy Research & Development, 2023. [Online]. Available: https://www.nrel.gov/solar/.

[21] EnergySage, Solar Batteries: What You Need to Know, 2022. [Online]. Available: https://www.energysage.com/solar/solar-energy-storage/solarbatteries/.

[22] WindSim, Understanding Wind Simulation: A Comprehensive Guide, 2023. [Online]. Available: https://www.windsim.com/understanding-windsimulation-guide.

[23] “How Voltage Drop Solutions Help Grid Operators Save Costs,” Ashley Edison, May 4, 2022. [Online]. Available: https://www.ashleyedison.com/2021/09/13/voltage-dropcompensation/.

[24] “Voltage Drop Calculator and Formulas Explained,” Pocket Sparky. [Online]. Available: https://pocketsparky.com/knowledgebase/voltage-drop-calculator-andformula/.

[25] “Voltage Drop Calculations- Part One,” Electrical Knowhow. [Online]. Available: http://www.electricalknowhow.com/2013/05/Voltage-Drop-Calculations.html.

[26] “Voltage Drop Calculations- Part Two,” Electrical Knowhow. [Online]. Available: http://www.electricalknowhow.com/2013/05/NEC-Method-for-Voltage-Drop-Calculations.html.

[27] “Voltage Drop Calculations- Part Three,” Electrical Knowhow. [Online]. Available: http://www.electricalknowhow.com/2013/05/NEC-Chapter-9-Tables.html.

[28] M. Maor and T. Reddy, Near Optimal Scheduling Control of Combined Heat and Power Systems for Buildings, Research Project 1340-RP, American Society of Heating, Refrigerating and Air-Conditioning Engineers, Atlanta, GA, USA, 2008.

[29] P. Bearn, “EPO: Emergency Power, Pure Power,” Winter/08, 2008.

[30] J. Mayer, “Saving Energy in an All-Fuel Plant,” Power, Oct. 1974.

[31] M. Krarti, Energy-Efficient Electrical Systems for Buildings, 1st ed. Moncef Krarti, 2016.

[32] Banco Popular, “Initial investment of the cogeneration plant at Cupey,” in Cogeneration Plant Analysis, Chapter 14: Economic Analysis, Table 14.2, p. 125.

[33] Banco Popular, “Energy cost before cogeneration at Cupey,” in *Cogeneration Plant Analysis*, Chapter 14: Economic Analysis, Table 14.10, p. 129.

[34] Banco Popular, “Post-cogeneration energy costs at Cupey,” in *Cogeneration Plant Analysis*, Chapter 14: Economic Analysis, Table 14.11, p. 130.

[35] Banco Popular, “Cost of LNG at Cupey,” in *Cogeneration Plant Analysis*, Chapter 14: Economic Analysis, Table 14.12, p. 130.

[36] Banco Popular, “Cost of LNG at Cupey,” in *Cogeneration Plant Analysis*, Chapter 14: Economic Analysis, Table 14.13, p. 131.

[37] D. Flin, Cogeneration: A User’s Guide, 11th ed., Institution of Engineering and Technology, 2009.

[38] R. Bartnik and Z. Buryn, “Conversion of Coal-Fired Power Plants to Cogeneration and Combined-Cycle,” Springer, Jul. 28, 2011.

[39] “What is cogeneration, its benefits and how does cogeneration work?” Cummins, Jun. 8, 2020. [Online]. Available: https://www.cummins.com/.

[40] “Combined Heat and Power,” Electrical4u, Oct. 25, 2020. [Online]. Available: https://www.electrical4u.com/.

[41] “Combined Heat and Power basics,” Energy.gov. [Online]. Available: https://www.energy.gov/.

[42] “Heat Recovery ventilation,” Wikipedia. [Online]. Available: https://en.wikipedia.org/wiki/Heat_recovery_ventilation.

[43] “Grounding Versus Bonding: Part 2,” ADE Learning. [Online]. Available: https://www.adelearning.com/.

[44] “Grounding Versus Bonding,” Jade Learning. [Online]. Available: https://www.jadelearning.com/wp-content/uploads/2018/08/Grounding2.png.